Probability and Inference in Forensic Science Research Paper

This sample Probability and Inference in Forensic Science Research Paper is published for educational and informational purposes only. If you need help writing your assignment, please use our research paper writing service and buy a paper on any topic at affordable price. Also check our tips on how to write a research paper, see the lists of criminal justice research paper topics, and browse research paper examples.

Various members of the justice system encounter uncertainty as an inevitable complication in inference and decision-making. Inference relates to the use of incomplete information (typically given by results of scientific examinations) in order to reason about propositions of interest (e.g., whether or not a given individual is the source of an evidential trace). In turn, judges are required to make practical decisions which represent a core aspect of their professional activity (e.g., deciding whether or not a given suspect is to be considered as the source of a given crime-related trace). Both aspects, inference and decision-making, require a logical assistance because unaided human reasoning is known to be liable to bias. From a methodological point of view, these challenges should be approached within a general framework that includes probability and (Bayesian) decision theory.

Introduction

Since the early 1960s, the forensic science community started to take a more explicit position with respect to the existence of a problem of interpretation and evaluation of data. In a now widely known quote, Kirk and Kingston from the University of California, Berkeley, note:

When we claim that criminalistics is a science, we must be embarrassed, for no science is without some mathematical background, however meagre. This lack must be a matter of primary concern to the educator [.. .]. Most, if not all, of the amateurish efforts of all of us to justify our own evidence interpretations have been deficient in mathematical exactness and philosophical understanding. (Kingston and Kirk 1964, pp. 435–436)

Today, interpretation and data evaluation are still held as a neglected area, mainly in fields that involve so-called physical evidence. This is acknowledged, for instance, by institutions such as the National Research Council (2009). In its report from 2009 (at pp. 6–3), the Council notes that “[t]here is a critical need in most fields of forensic science to raise standards for reporting and testifying about the results of investigations.” In many contexts, this perception is reinforced by the fact that scientists’ assessments of evidential value consist of a largely “subjective” component and a connotation of “arbitrary.” This should be contrasted, however, with an alternative interpretation that views the term “subjective” as a coherent state of personal belief held by an individual about something uncertain (see also Sects. 5 and 6).

As mentioned by Kirk and Kingston (1964), it was indeed rare at their time of writing – and it probably still is often so today – that a scientist’s opinion was based on a quantitative study. Besides some notable exceptions, such as forensic DNA (that is beyond the scope of this text), this is still so today even though the presentation of a general model for inference was already put forward by Darboux et al. (1908) and rediscovered later by Kingston (1965). In a more formal sense, that model is known in current days as the “Bayesian perspective” to reasoning and inference in forensic science.

It constitutes a main part of an approach to accepting that forensic science as well as science in general should abandon the expression of certainty. By moving away from the notion of certainty, it becomes a logical necessity to determine the degree of belief that may be assigned to a particular event or proposition of interest. In this context, the general branch of statistics can offer a valuable contribution to science. When uncertainty exists, and data are available, then it offers the possibility to assess and measure the uncertainty based upon a precise and logical line of reasoning (de Finetti 1993). Although statistics can offer a viable contribution to data evaluation by providing methods and techniques, it is not sufficient only by itself. Statistics concentrates primarily on data, whereas the retrospective meaning of an observation relies on the more general concept of inference which focuses on the notion of uncertainty. A concise expression of this is due to an influential writer in forensic interpretation, I. W. Evett, who noted that “[p]eople call this statistics – [but] it is not actually statistics, it’s inference, it’s reasonable reasoning in the face of uncertainty” (I. W. Evett, “Clarity or confusion? Making expert opinions make sense,” presentation held on June 24, 2009, at the event of his award of a Doctorate Honoris Causa, issued as part of the celebration of the 100th anniversary of the School of Criminal Justice of the University of Lausanne).

In view of these limiting aspects of contemporary uncertainty management in forensic science, this research paper will cover six arguments underlying the evaluation of forensic science data. First, Sect. 3 emphasizes the inevitability of uncertainty in day-to-day scientific work, followed in Sect. 4 by an outline of the necessity to deal with such a constraint through the use of a model that helps reasoners in a legal context – be they scientists or recipients of expert information – to manage the uncertainty about issues they are faced with. Next, probability and Bayes’ theorem are introduced as the essential ways of learning from experience, a process interpreted here as the updating of beliefs about an event of interest in the light of newly acquired information (Sect. 5). Some discussion is developed on how to interpret the notion of probability as a consequence of the use of the laws of probability. Section 6 introduces the personalistic (subjective) viewpoint which finds applications also beyond law and forensic science, such as economics and other scientific disciplines. A particular aspect of the probabilistic approach allows scientists to provide a measure of the value of forensic science data that a Court of Justice may incorporate in a more general framework of reasoning about ultimate target propositions. This is described in Sect. 7, followed by a general conclusion in Sect. 8. It reiterates the fundamental benefit of an approach (Bayesian) to deal with uncertainty as an indissociable feature of human activities in general.

This research paper avoids a dense presentation in terms of a list of mathematical formulae to deal with different forensic scenarios and scientific data as they may be encountered with, for example, DNA, shoe marks, glass and paint fragments, and textile fibers. Full treatises as given by, for instance, Aitken and Taroni (2004) and Buckleton et al. (2005), offer detailed formal developments of this kind. The perspective here is broader and seeks to offer a more general account on the relationship between inference, probability, and forensic science.

Uncertainty In Forensic Science

Human understanding of the past, the present, and the future is inevitably incomplete. This implies what is commonly referred to as a state of uncertainty, that is, a situation encountered by an individual with imperfect knowledge. Uncertainty is an indissociable complication in daily life, and the case of forensic science epitomizes this.

The criminal justice system at large, along with forensic science, is typically confronted with unique/singular events that happened in the past, which cannot be replicated. Due to spatial and temporal limitations, only partial knowledge about past occurrences is possible. Throughout history, this circumstance substantially troubled, and continues to do so, both scientists and other actors of the criminal justice system. This discomfort clearly illustrates the continuing need to give this outset a careful attention.

Despite this substantial drawback, “the problem of uncertainty” may not necessarily be considered as unsurmountable. Indeed, the careful reader may invoke the fact that past events leave one with distinct remains and vestiges, in particular, as a result of criminal activities. These may generate tangible physical entities such as blood stains, patterns, signals, glass fragments, or textile fibers that scientists may discover, seize, and examine. Results of such examinations have a potential for informing about and retracing past and ongoing events. Moreover, one may invoke developments in science and technology that offer vast capabilities for providing scientists with valuable information. While systematic analytical testing and observation may indeed produce abundant quantities of information, much of this information may substantively lack in qualities sufficient to provide an evaluative opinion that would be needed to entail (or make necessary) particular hypotheses that are of interest to legal reasoners.

A technocratic view of forensic science in terms of machinery and equipment under controlled laboratory settings is largely artificial. Actually, forensic science operates under a general framework of circumstances that makes testing and analyses a rather challenging undertaking. It suffices to note that material related to crimes and many other real-world events may often be affected by degradation or contamination. In addition, it may also be present in only low quantities so that only limited methods or measurements can be applied. A further aspect is that specimens submitted for laboratory analysis may be of varying relevance. In short, there is uncertainty about a true connection between the material at hand and the offense or the offender. In summary, thus, questions about laboratory performance are undoubtedly important, but they are not a general guard against the rise of uncertainty in attempts to reconstruct the past.

Generating data, observations, measurements, and counts constitute a core part of forensic science practice, but it is equally important to inquire about the ways in which such information ought – in the light of uncertainty – be used to modify a reasoner’s states of belief in a specific case. Legal actors have a natural interest in this inferential topic because it represents a vital step to guarantee that scientific information meaningfully serves the purpose of a particular application. This connects closely to the agreed requirement according to which procedures for learning about past events in the light of new information should be in some sense rational and internally consistent.

Scientific Inference And Induction

Learning from experience represents as much a fundamental problem of scientific progress as it presents one in everyday life. In part, experience leads to knowledge that is merely a description of what has already been observed. However, one can take this outset a step further and consider, based on past experience, prediction of future experience, referred also to as induction. Stated otherwise, on the basis of what one sees, one seeks to evaluate the uncertainty associated with a particular event of interest, even though this kind of reasoning for learning new things provides only an incomplete basis for a conclusion. In inductive reasoning, conclusions contain elements not present in the premises, and go beyond these premises, and this means that one’s knowledge is extended and the inference is said to be ampliative.

Humans tend to be well accommodated with operating under and dealing with situations involving uncertainty. Thus, the mere presence of uncertainty does not hinder the practice of science in principle. Accordingly, debates should focus on uncertainty explicitly and seek to distinguish between what is more likely and what is less likely, rather than attempting to endorse a concept of certainty. With that being said, the very relevant need of science is that of learning how to deal quantitatively with “probabilities of causes” (Poincare´ 1896). Indeed, a main aim of the experimental method is that of discriminating between events of interest, or “causes,” in the light of particular acquired information.

The so-called Bayesian theory (Sect. 5) claims that the inferential steps involved in inductive reasoning must be accomplished by means of probability, and in particular by means of Bayes’ theorem that shows how the probability assessments of future events are to be modified in the light of observed events. This is said to represent the meaning of the phrase “to learn from experience” in a mathematical formulation of induction (de Finetti 1972).

A Model For Inference: Bayes’ Theorem

As argued so far, learning from experience is central to scientific inference. According to a now widely accepted view, scientific reasoning essentially amounts to reasoning in accordance with the laws of probability theory (Howson and Urbach 1993) with Bayes’ theorem providing a solution to the general problem of induction. The latter is seen as an appropriate logical scheme for characterizing inferences designed to establish scientific case hypotheses. To state this more formally for a finite case setting, start by considering a set of mutually exclusive and exhaustive hypotheses H₁,.. .,H_n, the collection of background knowledge B, and a set of experimental results or effects E. Bayes’ theorem then says that the probability of a hypothesis of interest H_i, given E and B, is obtained as follows:

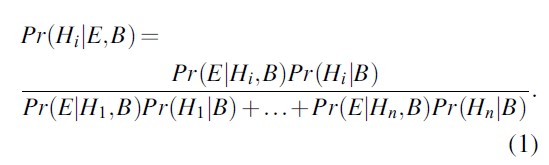
Broadly speaking, Bayes’ theorem tells one how to update prior beliefs (i.e., prior to data acquisition) about hypotheses in light of data. This leads one to posterior beliefs, that is, a state of belief after that data has been acquired.

It is worth emphasizing at this juncture that the conceptual meaning of a posterior belief is not that of a rectification. On this issue, de Finetti noted the following: “For convenience, brevity, and seeming clarity, I have just spoken of opinion as being ‘modified’. It would not be exact, however, to interpret this as ‘corrected’. The probability of an event conditional on, or in the light of, a specified result is a different probability, not a better evaluation of the original probability. [.. .] [p]robabilities are not corrections of the first one; each is the probability relative to a specific state of information [.. .]” (de Finetti 1972, at pp. 149–150).

In the above equation, the notation Pr represents “probability” and the vertical bar | denotes the conditioning. Thus, Pr(H_i|E,B) expresses the probability that Hi occurs, given that data E has occurred and background information is as described. This conditional probability of the given hypotheses Hi, after obtaining the data, is usually referred to as the posterior probability of H_i. In turn, Pr(H_i|B) is the corresponding prior probability of Hi, that is, before considering data E. Each probability is conditioned on the background knowledge B.

It is possible to consider an effect E also in terms of its influence on the belief about the truth or otherwise of a hypothesis, say H, that is:

• E confirms or supports H when Pr(H|E,B)> Pr(H|B).
• E disconfirms or undermines H when Pr(H|E,B)< Pr(H|B).
• E is neutral with respect to H when Pr(H|E,B) = Pr(H|B).

One can thus interpret the difference Pr(H|E, B)- Pr(H|B) as a measure of the degree with which E supports H, and Bayes’ theorem constitutes a logical scheme to understand how the observation of an effect supports or undermines hypotheses. On a conceptual account, Jeffrey (1975) has noted the following:

Bayesianism does not take the task of scientific methodology to be that of establishing the truth of scientific hypotheses, but to be that of confirming or disconfirming them to degrees which reflect the overall effect of the available evidence positive, negative, or neutral, as the case may be. (at p. 104)

For applications in forensic science, it is common to consider hypotheses in pairs. For example, H₁ may denote the hypothesis proposed by the prosecution, while H₂ denotes the hypothesis proposed by the defense. In such a setting, an alternative version of Bayes’ theorem, known as the odds form, is often used. In that version, H2 denotes the complement of H₁ so that Pr(H₂)=1-Pr(H₁). Then, the odds in favor of H₁ are Pr(H₁)/Pr(H₂), denoted O(H₁), and the odds in favor of H₁ given E are denoted O(H₁|E). Note that the conditioning on B is omitted for simplicity of notation. The odds form of Bayes’ theorem then is

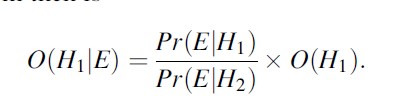
The left-hand side of this equation is the odds in favor of the “prosecution” hypothesis H₁ after the scientific evidence has been presented, O(H₁|E). This is referred to as the posterior odds. The odds O(H₁) are the prior odds as held by a reasoner before considering the observation. The ratio which converts prior odds to posterior odds is the fraction

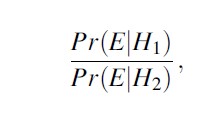
known as the Bayes’ factor, or often also called likelihood ratio. It is commonly denoted by the letter V, short for “value.” It can take values between 0 and ∞. A value greater than 1 lends support to the prosecution’s hypothesis H₁ and a value less than 1 lends support to the defense’s hypothesis H₂. Effects for which the value is 1 are neutral, that is, it does not allow one to discriminate between the two competing hypotheses. Note that if logarithms are used, the relationship becomes additive. This has the very appealing and intuitive interpretation of weighing evidence in the scales of justice. In statistical literature, the logarithm of the Bayes’ factor became known as the weight of evidence and is generally acknowledged to Good (1950).

In forensic and legal settings, the value of scientific data is most beneficially assessed by finding a value for the Bayes’ factor, a task commonly assigned to forensic scientists. In turn, it is the role of judge and jury to assess the prior and posterior odds. In this view, the scientist can assess how prior odds are altered by the evidence, but he cannot actually assign a value to the prior or posterior odds. In order to assign such a value, all the other evidence in the case also needs to be considered. Although the adequacy of such a perspective continues to be debated in both literature and practice, this tends to be less the case today than during the past decades (Redmayne et al. 2011). Probably, it is also fair to say that there currently appears to be no other method that is of better overall assistance to evidential reasoning in judicial contexts. This is maintained, for example, by Ian W. Evett, a pioneer forensic statistician, who has been quoted as saying (Joyce 2005, at p. 37), “That framework – call it Bayesian, call it logical – is just so perfect for forensic science. All the statisticians I know who have come into this field, and have looked at the problem of interpreting evidence within the context of the criminal trial, have come to see it as centring around Bayes’s Theorem.” It is not claimed, however, that Bayesian inference is a panacea for all problems in legal reasoning. But it can be maintained that it is the best available model for understanding the interpretation of scientific evidence.

Besides discrete propositions, forensic scientists may also need to deal with continuous parameters. Examples include the mean of a continuous variable or a proportion. For such applications, Bayes’ theorem as defined in Eq. (1) takes a slightly different form. In the context, an unknown parameter is commonly written Y and data available for analysis as y = (y₁,.. .,y_n). In the case of a continuous parameter, beliefs are represented as probability density functions. Denoting the prior distribution as p(Y) and the posterior density as p(Y|y), Bayes’ theorem for a continuous parameter is

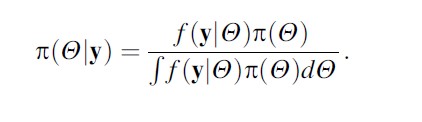
Subjective Probabilities In The Bayesian Model

Independent of the way in which probabilities are interpreted, they take values in the range between 0 and 1. The value 0 corresponds to an event whose occurrence is impossible. An event whose occurrence is certain has probability 1. In a common, and for various reasons appropriate, interpretation of the theory, all probabilities are considered as subjective – in the sense of “personal” – expressions of degree of belief, held by an individual. Probabilities thus reflect the extent to which an individual’s knowledge is imperfect, and it is important to acknowledge that such personal belief is graduated. One can believe in the truth of an event more or less than at another one at a given time, essentially because observations can accumulate to modify the perception of the probability of its happening.

A main aspect of this interpretation is that the degrees of belief held by an individual, in order to be said “rational,” need to conform to the rules of probability. As such, probability represents the quantified judgment of a particular individual. This is in opposition to other interpretations of probability, known, for example, as the “classical” or “frequentist” interpretations that consider probability in terms of a long-run frequency. These latter views may encounter problems in applicability when settings refer to non-repetitive or singular situations (Press and Tanur 2001). Indeed, the frequentist view strictly supposes a relative frequency obtained in a long sequence of trials that are assumed to be performed in stable conditions and physically independent of each other. This is typically incompatible with events and parameters encountered in such diverse fields such as history, law, economy, forensic science, and other contexts where inductive inference plays a central role. In the latter branches, the entities of interest are usually not the result of repetitive or replicable processes. On the contrary, they are singular and unique, and this makes the idea of repeating the course of time over and over again, and to note the number of occasions on which some happening in the past occurred, inconceivable.

Such complications do not arise with the personalistic interpretation because it does not consider probability as a feature of the external world, but as a notion that describes the relationship between a person issuing a statement of uncertainty and the real world to which that statement relates, and in which that person acts. For the belief-type perspective, it is therefore perfectly reasonable to assign probability to non-repeatable events. This feature renders probability as a measure of belief a particularly useful concept for judicial contexts.

An direct implication of considering probability as personal degree of belief is that the knowledge, experience, and information on which the individual at hand relies become important. That is, more explicitly formulated, an individual’s assessment of the truth of a given statement or event (i) depends on information, (ii) may change as the information changes, and (iii) may vary among individuals because different individuals may have different information or assessment criteria.

Although this perspective most closely embraces the actual situation faced by an individual in a situation of uncertainty, personal probabilities are sometimes viewed cautiously. As a concept, it may appear abstract and nontrivial to capture, and typically scientists may be irrationally suspicious of articulating, yet admitting to hold genuine subjective probabilities. In the same context, people may also be reluctant to express probabilities numerically and suggest that this approach to probability is both arbitrary and, from a practical point of view, an inaccessible concept. Such perceptions are restrictive because they disregard the fact that personal degrees of belief can be elicited and investigated empirically. One possibility to effectuate this is to measure probabilities maintained by an individual in terms of bets that the individual is willing to accept. For example, an individual’s probability of a proposition can be elicited by comparing two lotteries of the same price.

In order to illustrate the usefulness of such a procedure for quantifying judgments, consider a situation in which it is of interest to find a probability for rain tomorrow (Winkler 1996, e.g.; at 18). For this purpose, define the following two offers:

• Lottery A: Winning € 100 with probability 0.5, and winning € 0 with probability 0.5
• Lottery B: Winning € 100 if it rains tomorrow, and winning € 0 if it does not rain tomorrow

With this outset, one can assume that one would choose that offer which presents the greater chance of winning the price. Clearly, if one prefers Lottery B, then this signifies that one considers the probability of rain tomorrow to be greater than 0.5. By analogy, choosing Lottery A would imply that one’s belief in rain tomorrow is lower than 0.5. Moreover, in a case in which one is indifferent between the two gambles, one’s probability for rain tomorrow would equate the probability of winning the price in Lottery A. Therefore, one can conceive of a procedure in which one adjusts the chance of winning in Lottery A so that the individual, whose probability for a proposition of interest is to be elicited, would be indifferent with respect to Lottery B. Similarly, one can elicit an individual’s personal probability for any event of interest.

Another question relates to the “appropriateness” of a set of probabilities held by a particular individual. In this context, the possibility of representing subjective degrees of belief in terms of betting rates is often forwarded as part of a line of argument to require that subjective degrees of belief should satisfy the laws of probability. This line of argument takes two steps. The first one of these proposes that betting rates should be coherent, in the sense that they should not be open to a sure-loss contract.

The second one is given by the fact – established by twentieth-century writers in probability (e.g., Ramsey 1990) – that a set of betting rates is coherent if and only if it satisfies the laws of probability. Thus, if an individual assigns degrees of belief in such a manner that, as a whole, they do not respect the laws of probability, then their beliefs are not coherent. In the context, such incoherence is also called “logical imprudence.”

The Bayesian Model And The Desiderata For Evidential Assessment And Interpretation

In the context of framing scientific evaluation in legal contexts, scientists and jurists wish their analytical thoughts and behavior to conform to several practical precepts, and interestingly, the Bayesian model allows to conceptualize these precepts explicitly. It is common to refer to essentially six desiderata upon which the majority of current scientific and legal literature as well as the practice converge in their opinion, namely, balance, transparency, robustness, added value, flexibility, and logic. These notions represent desirable properties of an evaluative procedure for scientific opinions. They have been advocated and contextualized, to a great extent, by some quarters in forensic science and from jurists from the so-called New Evidence Scholarship.

For an inferential process to be balanced or, in the words of some authors, impartial, attention cannot be restricted to only one side of an argument. Evett (1996) has noted, for instance, that “[.. .] a scientist cannot speculate about the truth of a proposition without considering at least one alternative proposition. Indeed, an interpretation is without meaning unless the scientist clearly states the alternatives he has considered.” The requirement of considering alternative propositions is a general one that equally applies in many instances of daily life (Lindley 1985), but in legal contexts, its role is fundamental. The Bayesian framework allows one to cope with this requirement in an integral way as it provides for an explicit treatment of a collection of rival propositions within a coordinated whole.

The proposal of considering alternatives should not be taken to mean, however, that scientist should address propositions in terms of probability. This is a task left to other legal actors as mentioned earlier in Sect. 5. A likelihood ratio-based approach for ascribing evidential value suggests that forensic scientists should primarily be concerned with their observations and results and not with the competing propositions that are put forward to account for such data. This distinction is crucial in that it provides for a sharp demarcation of the boundaries of the expert’s and the court’s areas of competence. Failures in recognizing that distinction are at the heart of pitfalls of intuition that have caused – and continue to cause – much discussion throughout the judicial literature and practice since (e.g., Koehler 1993).

Besides balance, a forensic scientist’s evaluation should also comply with the requirement of transparency. This amounts to explain in a clear and explicit way what scientists have done, why they have done it, and how they have arrived at their conclusions. Closely related to this is the notion of robustness, which challenges a scientist’s ability to explain the grounds for his opinion, together with his degree of understanding of the particular data type. These elements should help work towards added value, that is, a descriptor of a forensic deliverable that contributes in some substantial way to a case. Often, added value is a function of time and monetary resources, deployed in a way such as to help solve or clarify specific issues that actually matter with respect to a given client’s objectives. These desiderata characterize primarily the scientist, that is, his attitude in evaluating and offering opinions, as well as the product of that activity.

The degree to which the scientist succeeds in meeting these criteria depends crucially on the chosen inferential framework, which may be judged by the two criteria flexibility and logic. These descriptors relate to properties of an inferential method rather than behavioral aspects of the scientist as mentioned in the previous paragraph. In a broad sense, flexibility is a criterion that demands a form of reasoning to be generally applicable, that is, not limited to particular subject matter (Robertson and Vignaux 1998). In turn, logic refers to a set of principles that qualify as “rational.” There is a broad agreement among legal and forensic researchers and practitioners that the Bayesian framework for reasoning acceptably complies with these requirements nowadays. On a conceptual account, this view is supported by the fact that the paths of reasoning used to evaluate propositions in judicial contexts can be reconstructed as inferences in accordance with Bayes’ theorem.

General Appreciation And Outlook

As a key point, probability is shown to be a formal quantitative framework with solid logical grounds that usefully assists legal actors, including forensic scientists, to make plain inferential subtleties that common language and unaided intuitive reasoning cannot achieve and to explain these issues. In this general framework, it is preferable to employ probability as degrees of belief, a standpoint commonly known as the subjectivist (or personalist) interpretation of probability. Such degrees of belief are personalized assessments of credibility formed by an individual about something uncertain, given information that the individual knows or can discover. This usage of the probability apparatus implements a concept of reference in which personalized weights may be assigned to the possible states of selected aspects of real-world problems. This closely embraces the actual situation encountered by legal practitioners. Even though uncertainty is inevitable in principle, the position of legal actors is one which allows at least some further evidence to be gained by enquiry, analysis, and experimentation. As a consequence of this, some means is required to adjust existing beliefs in the light of new information.

As a second main element, this research paper favors the requirement of adjusting personal beliefs according to Bayes’ theorem, essentially because it is a logical consequence of the basic rules of probability. This perspective is normative, in the sense that if one accepts the laws probability as constraints to which one’s beliefs should conform, then one also needs to accept the ensuing properties – among which is Bayes’ theorem. Interpreting these rules as a norm, or a standard, allows for a prescription of how a sensible individual ought to reason, to behave, or to proceed. Although practical experience shows that people in general, including scientists, may not conform well in their reasoning with the laws of probability – in fact, descriptive studies actually show that people’s intuitive judgments diverge from the probability standard – the argument is that the concept should guide in the inferential processes in which one engages. It provides a defensible framework that allows one to understand how to treat new information, how to critically analyze, and how to revise opinions in a coherent way.

Arguably, probability as a measure of uncertainty takes the role of fundamental quality criteria in forensic science. The benefits of a probabilistic framework are both immediate and uncontroversial because of the direct effect that uncertainties may have on a line of reasoning which matters in some way to an evaluator or decision maker.

From a historical perspective, Bayes’ (1702–1761) theorem came about 250 years ago, but the attribute “Bayesian” as a descriptor of a particular class of inference methods appears to have gained more widespread use only since the middle of the twentieth century (Fienberg 2003). In the legal context, there now is a growing community that has spent many years applying Bayesian principles to infer from evidence. This interest in Bayes’ theorem is reinforced because of its supportive capacity in explaining the concept of evidence and proof in both science and law and other inferential contexts, but also because formal procedures can be easier to explain and justify than informal ones.

Still within a historical perspective, practical applications of patterns of reasoning corresponding to a Bayesian approach can be found, for example, as early as the beginning of the twentieth century (Taroni et al. 1998). For example, at the Dreyfus’s military trial held in 1908, Henri Poincare´ invoked Bayes’ theorem as the only way in which the court ought to revise its opinion about the issue of forgery. Subsequently, Bayesian ideas for inference entered legal literature and debates more systematically only in the second half of the twentieth century. Kingston (1965), Finkelstein and Fairley (1970), and Lindley (1977) are some of the main reference publications from that period. Later, within the 1990s, specialized textbooks from Aitken and Stoney (1991) and Robertson and Vignaux (1995) appeared. During the past decade, further textbooks along with a regular stream of research papers focusing on Bayesian evaluations of particular categories of evidence, such as glass or DNA (Buckleton et al. 2005) were published. But yet, if one looks at science more generally, the interest in Bayesian methods to solve problems relating to data analysis appears to be relatively scarce, with forensic science being no exception (Taroni et al. 2010).

Although much of the current discussion essentially focuses, in one way or another, on the evaluation and manipulation of personal beliefs held in propositions about which one is uncertain, reality shows that what one believes is essential, but not only in its own right. Along with a reasoner’s preferences, personal beliefs – typically expressed in terms of probabilities – are a fundamental ingredient of considerations that seek to analyze what one ought to decide. Indeed, for the criminal justice system, reasoning about propositions of interest is not the end of the matter. It is commonly understood that, ultimately, decisions must be taken and that these are at the heart of judicial proceedings. For instance, a court may have to decide if it finds a suspect guilty of the offense for which he has been charged, with the obvious aim that such decisions are made accurately (Kaplan 1968). In this broader perspective, probability can be taken as a preliminary to decision-making. On a formal account, this logical extension is embedded in decision theory, which provides the means for dealing with the key elements of decision analysis processes. Since both forensic scientists and recipients of expert information encounter the recurrent need to decide on matters that relate to their respective areas of competence, Bayesian decision analysis represents a topic of ongoing interest. Although its relevance from a legal point of view has already been recognized decades ago (e.g., Kaplan 1968; Lempert 1977), it is only more recently that genuine forensic applications (Taroni et al. 2005; Biedermann et al. 2008) have been approached.

Bibliography:

1. Aitken CGG, Stoney DA (1991) The use of statistics in forensic science. Ellis Horwood, New York
2. Aitken CGG, Taroni F (2004) Statistics and the evaluation of evidence for forensic scientists, 2nd edn. Wiley, Chichester
3. Biedermann A, Bozza S, Taroni F (2008) Decision theoretic properties of forensic identification: underlying logic and argumentative implications. Forensic Sci Int 177:120–132
4. Buckleton JS, Triggs CM, Walsh SJ (2005) Forensic DNA evidence interpretation. CRC Press, Boca Raton
5. Darboux JG, Appell PE, Poincare´ JH (1908) Examen critique des divers syste`mes ou e´tudes graphologiques auxquels a donne´ lieu le bordereau. In: L’affaire Dreyfus – La re´vision du proce`s de Rennes – Enqueˆte de la chambre criminelle de la Cour de Cassation. Ligue franc¸aise des droits de l’homme et du citoyen, Paris
6. de Finetti B (1972) Probability, induction and statistics. Wiley, New York
7. de Finetti B (1993) The role of probability in the different attitudes of scientific thinking. In: Monari P, Cocchi D (eds) Bruno de Finetti, Probabilita` e induzione. Bibliotheca di STATISTICA, Bologna, pp 491–511, 1977
8. Evett IW (1996) Expert evidence and forensic misconceptions of the nature of exact science. Sci Justice 36:118–122
9. Fienberg SE (2003) When did Bayesian inference become “Bayesian”? Bayesian Anal 1:1–41
10. Finkelstein MO, Fairley WB (1970) A Bayesian approach to identification evidence. Harv Law Rev 83:489–517
11. Good IJ (1950) Probability and the weighing of evidence. Griffin, London
12. Howson C, Urbach P (1993) Scientific reasoning: the Bayesian approach, 2nd edn. Open Court, La Salle
13. Jeffrey RC (1975) Probability and falsification: critique of the popper program. Synthese 30:95–117
14. Joyce H (2005) Career story: consultant forensic statistician. Communication with Ian Evett. Significance 2(34–37):2005, March 2005
15. Kaplan J (1968) Decision theory and the factfinding process. Stanf Law Rev 20:1065–1092
16. Kingston CR (1965) Application of probability theory in criminalistics – II. J Am Stat Assoc 60:1028–1034
17. Kingston CR, Kirk PL (1964) The use of statistics in criminalistics. J Crim Law Criminol Police Sci 55:514–521
18. Koehler JJ (1993) Error and exaggeration in the presentation of DNA evidence at trial. Jurimetrics J 34:21–39
19. Lempert RO (1977) Modeling relevance. Mich Law Rev 75:1021–1057
20. Lindley DV (1977) Probability and the law. Statistician 26:203–220
21. Lindley D (1985) Making decisions, 2nd edn. Wiley, Chichester
22. National Research Council (2009) Strengthening forensic science in the United States: a path forward. National Academy Press, Washington, D.C
23. Poincare´ H (1896) Calcul des probabilite´s. Lec¸ons professe´es pendant le deuxie`me semestre 1893–1894. Gauthier-Villars, Paris
24. Press SJ, Tanur JM (2001) The subjectivity of scientists and the Bayesian approach. Wiley, New York
25. Ramsey FP (1990) Truth and probability. In: Mellor DH (ed) Philosophical papers. Cambridge University Press, Cambridge, pp 52–109, 1926
26. Redmayne M, Roberts P, Aitken CGG, Jackson G (2011) Forensic science evidence in question. Crim Law Rev 5:347–356
27. Robertson B, Vignaux GA (1995) Interpreting evidence. Evaluating forensic science in the courtroom. Wiley, Chichester
28. Robertson B, Vignaux GA (1998) Explaining evidence logically. N Law J Expert Witn Suppl 148:159–162
29. Taroni F, Champod C, Margot P (1998) Forerunners of Bayesianism in early forensic science. Jurimetrics J 38:183–200
30. Taroni F, Bozza S, Aitken CGG (2005) Decision analysis in forensic science. J Forensic Sci 50:894–905
31. Taroni F, Bozza S, Biedermann A, Garbolino G, Aitken CGG (2010) Data analysis in forensic science: a Bayesian decision perspective. Wiley, Chichester
32. Winkler RL (1996) An introduction to Bayesian inference and decision. Probabilistic Publishing, Gainesville

See also:

• How to Write a Research Paper
• Research Paper Topics
• Research Paper Examples

Free research papers are not written to satisfy your specific instructions. You can use our professional writing services to buy a custom research paper on any topic and get your high quality paper at affordable price.