Randomized Block Designs Research Paper

This sample Randomized Block Designs Research Paper is published for educational and informational purposes only. If you need help writing your assignment, please use our research paper writing service and buy a paper on any topic at affordable price. Also check our tips on how to write a research paper, see the lists of criminal justice research paper topics, and browse research paper examples.

Experimental criminologists pay close attention to baseline equality between the treatment and control groups. When the study groups are not similar to one another, this introduces biases and confusion in the interpretation of the treatment effect. Often simple random assignment procedures are used to create similar groups, treatment and control conditions. However, research shows that this simple process does not always work. By chance alone, one group can be larger and have more of a particular type of participants or type of traits. Such instances make it difficult to compare “like with like,” which is one of the cornerstones of randomized controlled trials. Instead, experimentalists and statisticians advise using randomized block designs, in which cases are randomly assigned within homogeneous blocks of participants, rather than from the overall sample. The variance within the blocks is minimized, which decreases the experimental “noise” and increases the statistical power of the test. Randomized block designs can also be used to “force” size equality in order to create exactly the same group sizes, something which cannot be done with simple random assignment. Below, instances in which it is optimal to use randomized block experiments are discussed, as well as how to design them, and the obstacles to avoid when using these designs. The general type of randomized block designs is introduced, along with two special cases: permuted randomized block designs and matched pairs, which are useful in small-scale studies where group-size equality is particularly important and when unmasking of the random allocation sequence does not create a source of concern.

Introduction

In randomized controlled trials, the experimental and control groups should be as similar to one another as possible. Without this equality prior to the administration of the treatment to the experimental group and not to the control group, the advantages of the experimental approach are dramatically diminished. Therefore, researchers conducting randomized controlled trials pay particularly close attention to the way cases are assigned to the treatment conditions of the study and work hard to preserve the integrity of this process, in both the design and implementation of the study.

Such balance – or group comparability – is achieved using a process of random allocation of cases into treatment and control groups. Probability theory predicts that the equal chance of each case to be assigned to either treatment or control conditions (e.g., a 50-50 chance) creates two groups that are likely to be similar to one another – except for the intervention that “experimental participants” are exposed to but “control participants” are not. Because participants are assigned to groups by chance, the likelihood that the experimental group will turn out to be different from the control group is significantly minimized when compared with a nonrandom assignment procedure. Therefore, any baseline traits that could explain the relationship between the treatment and outcome are equally divided between the two study groups, and the potential effect of these traits is believed to be controlled for by this design. Thus, the only explanation for any difference in outcomes between the experimental and control groups ought to be attributable to the treatment effect, and nothing else.

In practice, researchers use various techniques to produce a random assignment sequence. The most popular of these techniques is simple random assignment, in which the researcher divides the entire sample into two (or more) groups, using a basic algorithm. For example, if there are 200 cases in a particular study, 100 would receive the treatment, and 100 would serve as the control participants – and that assignment to the two groups is completely random. All statistical software packages, including various online calculators, can easily produce a random assignment sequence that would enable the researcher to allocate his or her cases in such a way.

However, while this simple random assignment procedure is likely to provide an overall balance, equality is not guaranteed. The risk of creating unequal groups still exists, despite the random assignment, when the allocation is not restricted. Unbalance can become a problem in the form of unequal group sizes (e.g., 90 compared to 110 participants) or one group “holding” more participants with a particular trait (e.g., more females than males or more motivated participants in one study group than the other). These problems can be quite concerning, and a large body of literature has tried to deal with these issues over the years (see Ariel and Farrington 2010; Weisburd and Taxman 2000). For example, unbalance is usually associated with a lower statistical power of the research design (see Lipsey 1990; Weisburd and Taxman 2000), particularly in small samples. This means that the ability of the test to show there are indeed differences between the study groups because of the intervention is greatly diminished. It has also been shown that interpreting the results from an unbalanced trial may lead to reaching biased conclusions about the true outcome effect of the tested intervention (Torgerson and Torgerson 2003).

The Randomized Block Design

Understanding that simple random assignment cannot guarantee the necessary balance between the groups has led researchers to try and anticipate and overcome the problem, and certain measures can now be taken to address it. Some are more successful than others. For example, it was (and perhaps still is) commonly assumed that increasing the size of the sample is associated with more balance and, in turn, with greater statistical power. But, as Weisburd et al. (1993) have shown, there are instances in which there can be an inverse relationship between sample size and statistical power. Especially in heterogeneous samples, larger samples are likely to include a wider diversity of participants than smaller investigations. Because it is necessary to establish very broad eligibility requirements in order to gain a larger number of cases, large trials tend to attract a more diverse pool of participants. This increases the variability in the data as there is more “noise,” which makes it difficult to detect the effect of the treatment. Therefore, the design benefits of larger trials may be offset by the implementation and management difficulties they present.

Given Weisburd et al.’s (1993) and similar research findings, along with a broader understanding of the shortcomings of simple random assignment, clinicians and statisticians have developed other research designs to more adequately handle unbalanced groups or high variability. One type which is slowly gaining recognition and is being applied more and more in experimental criminology is called the randomized block design. The concept behind randomized block designs is generally straightforward: if the researcher knows before he or she administers the treatment that certain participants may vary in significant ways, this information can be utilized to his or her advantage. The researcher can use a statistical design in which all participants are not simply randomly allocated directly into experimental and control groups. Instead, they are randomly allocated into groups within blocks.

The randomized block design is used in order to decrease the variance in the data (Lachin 1988). Unlike simple random assignments, where units are unrestrictedly distributed at random to either treatment or control groups (or more than two groups, as the case may be), units in a randomized block design are allocated randomly to either treatment or control within pre-identified blocks. The blocking process is established based on a certain criterion, which is intended to divide the sample, prior to assignment, into subgroups that are more homogeneous (Hallstrom and Davis 1988). Then, within these blocks, units are randomly assigned to either treatment or control conditions.

Variations of this design were implemented in some of the most influential studies in criminal justice research, particularly in place-based criminology, such as the Jersey City Problem-Oriented Policing Experiment at violent places (Braga et al. 1999). Recently, Weisburd et al. (2008) have used this design in an experiment on the effects of the risk-focused policing at places (RFPP) approach to preventing and reducing juvenile delinquency. Before administering the treatment, they found considerable variability in the characteristics of violent places selected for the study, which jeopardized the statistical power of the evaluation. In this case, the impact of the treatment will be more difficult to detect when there is a large variability in the assessment of study outcomes. The data were thus more adequately managed under a randomized block design. As in other hot-spot experiments (e.g., Ariel and Sherman forthcoming), the randomized block design is advantageous because it decreases the variations that characterize places, such as the drug activity, and structural and cultural characteristics. In several hotspots experiments, it was found that an examination of the distribution of arrest and call activity in the hot spots before the experiment revealed that the places fell into distinct groups – for example, high, medium, and low criminal activity blocks. Therefore, hot spots randomly allocated to experimental and control conditions within each of these conditions created more homogeneous groups of hot spots.

Randomized block designs can be used in person-based experiments as well. Similar issues arise in analyses of individuals in schools, prisons, and other environments, and so blocks can be created in these studies as well (see, e.g., Ttofi and Farrington 2012). For example, a large randomized controlled trial was conducted to test the hypothesis that differences in wording of letters sent to taxpayers in Israel would affect various aspects of their taxpaying behavior, such as the amount of money they were willing to report and pay to the tax authority (Ariel 2012). Nearly 17,000 taxpayers were randomly assigned to different groups, each receiving a different type of letter. However, a large sample of taxpayers introduced high variability. For example, the sample included very poor taxpayers as well as very rich taxpayers. The size of the sample also increased the likelihood that, in one of the study groups, there would be a disproportionally larger number of extremely rich taxpayers, so their effect on the results could skew the conclusion. Therefore, the sample was divided, before random assignment, into blocks of income levels. Within each of these income-level blocks, the participants were then randomly allocated into the different letter groups. Therefore, this procedure allows for measurement of not only the overall effect of letters but also of specific effects within the blocks (i.e., effect of letters on participants with different income levels).

Designing A Randomized Block Experiment

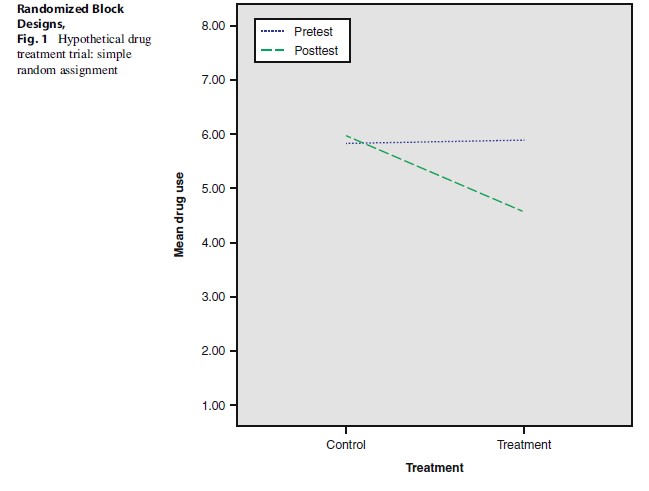
Consider the following hypothetical trial as a way to show the benefits of blocking and when this design should be considered. Imagine a trial with one experimental group consisting of 52 drugaddicted offenders, treated in an antidrug program. Another group of 48 drug-addicted offenders serve as the control group, receiving no drug treatment. The allocation to treatment and control is done randomly. The experiment is conducted in order to evaluate the merits of the program, where success is nominally defined by a decrease in drug use (on a scale of 1–8, 8 being the highest and 1 being the lowest). However, unlike other drug treatment programs, this particular treatment is very costly. Therefore, unless very high success rates are registered, the facilitators will be unlikely to recommend its implementation in the future. All eligible participants selected for this trial are known to be drug abusers before entering the program. Prior to the treatment, the drug use level was not statistically different between the two groups (both averaging about 5.85 on the said scale).

At the 6-month follow-up period, drug use was measured again for both groups. Results show that the program was successful: there was an overall 15 % reduction in the treated experimental group, when compared with the untreated control group. A visual depiction is presented in Fig. 1. At the same time, considering the costs of the program and that there was “only” a 15 % reduction, the policy implication is to not recommend further implementation of the program.

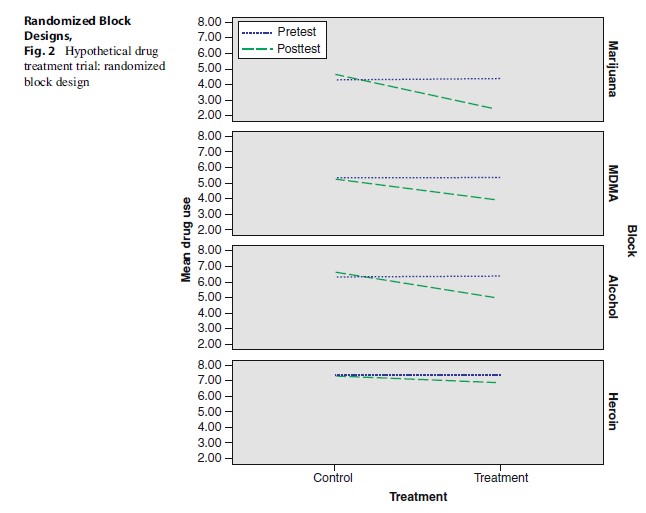
Randomized Block Designs Research Paper

However, a closer look at the distribution of the pretest scores indicates that the sample is comprised of drug abusers of four different types of drugs (with no crossovers): marijuana, MDMA, alcohol, and heroin. Generally speaking, it could be hypothesized that drug abusers of these different drugs are not addicted in the same way (based on both pharmacological and psychobiological qualities of these substances). Therefore, the prospective success rate of the drug intervention program is also hypothesized to be different for each subgroup; it is likely that getting clean from a heroin addiction or alcohol addiction is more difficult than from marijuana or MDMA. Thus, dividing the overall sample based on the type of drug should produce more homogeneous subgroups, whose chance to get clean is different.

One primary advantage of looking at the study this “blocked” way is that even if the strength of the treatment effect within each block is similar, more precise estimates of the magnitude of the treatment effect can be discovered because the intra-block variance is reduced. Because the “treatment estimate” is comprised of both the drug program and the variability, the treatment effect is likely to be larger within each block when the “noise” is reduced. It therefore becomes “easier” to see the effect, because the variance is reduced by the creation of homogeneous subgroups.

With this in mind, imagine another experiment, which is substantially similar to the one above: the treatment is delivered in the very same intensity and method as in simple random assignment, to a similar group of participants. However, the participants are grouped within “blocks of drug type,” which creates blocks of participants who are likely to be more similar to one another, at least in terms of the type of drug to which they are addicted.

Notice that the overall 15 % reduction compared to the control group is still expected to be registered. This is depicted in Fig. 2. As can be seen, the overall treatment-to-control magnitude of difference is the same across blocks. However, the intra-block reduction is different, because there is less variance in the data. The blocking procedure shows that the Heroin Block is less receptive to the treatment (6 % decrease in drug use), as arguably expected from this subgroup, compared, for example, to the Marijuana Block or the MDMA Block (51 % and 34 % decrease, respectively). Given such findings, the policy implication could then be to continue using the program for certain types of addictions in light of the high success rate, but not for others with a lower success rate.

Randomized Block Designs Research Paper

Planning Randomized Block Designs

When designing randomized block experiments, particular attention is drawn to three elements: the treatment effect (and the variance associated with it), the blocking criterion (i.e., the variable which divides the sample prior to random assignment), and the interaction between the treatment factor and the blocking factor – though the latter is generally ignored in criminal justice research and therefore omitted from the discussion. There are different ways to “block” the study participants, depending on the type of study. The blocking criterion is usually based on the natural cutoff points of the outcome variable of interest, at its baseline level – for example, the number of police calls for service in hot-spot experiments (e.g., Ariel and Sherman forthcoming). The blocking criterion can be nominal or categorical as well, such as gender, ethnicity, or crime type.

The model can be extended to account for several treatments and several blocks. However, there are a limited number of interventions that one research project can study. It seems that using only one treatment and one control condition in each block is more effective, because the test statistic becomes more “stable” than with multiple conditions and blocking criteria. At the same time, it is not clear how many blocking factors should be allowed before the design becomes too “messy” – though Friedman et al. (1985, p. 69) understandingly claimed that, for studies of 100 participants, blocking using up to 3 factors is still considered manageable.

It is most important that each block should contain all treatments and that each treatment should occur an equal number of times in each block (Chow and Liu 2004, pp. 136–140). Many of the experiments on policing crime in places are constructed in this way, such as the ones reviewed in the introduction.

As in all experiments, it is desirable that the administration of the treatment in terms of potency, consistency, and procedures is identical in each block. This means that the overall experimental design is replicated as many times as there are blocks, and each block can be viewed as a disparate yet identical trial within the overall study (Rosenberger and Lachin 2002). If the administration of the treatment was different in each block, it would be rather difficult to analyze the treatment effect. Therefore, maintaining the same treatment across the study blocks is advised.

Lastly, randomized block designs were found to be particularly advantageous when there are “several hundred participants” (Friedman et al. 1985, p. 75), but recent studies suggest that randomized block designs can also be useful in much smaller studies, especially in place-based experiments, in which the unit of analysis is geographical areas rather than human participants (see review in Gill and Weisburd 2013).

Permuted Randomized Block Design

The design presented earlier reduces the variance in the data caused by certain prognostic or other general variables. However, these models are less useful to address time-related biases created by sequential assignment of units. There are times when the researcher needs to achieve near-equality in the number of units assigned in each block to different treatments, at any stage of the recruitment process, not only at the end of the study. A special type of block randomized design is required to achieve this.

First introduced by Hill (1951; see Armitage 2003), the “permuted randomized block design” (PRBD) was developed in order to deal with these conditions. The PRBD is most appropriate when there is a strong need for both periodic and end-of-the-experiment balance in the number of participants assigned to each study group in each block. This is the case, for example, in small studies, or studies with many small subgroups (Rosenberger and Lachin 2002, pp. 41–45).

Suppose that a care provider cannot wait for more victims of a similar type to surface, in order to provide them with much-needed services at the same time (for instance, group counseling). This is a small study, with only 40 participants, so it is important to have an equal assignment of cases to treatment and control conditions. Furthermore, the treatment must be delivered as soon as possible. However, the simple random assignment procedure is not optimal, because of the increased threats such as selection bias and chronological bias (Kao et al. 2007, p. 364). A PRBD model can be used instead. With 40 participants, the researcher can break the sample up into 10 blocks, with 4 participants in each block, and one treatment group (T) and one control group (C). In each block, there are exactly six possible arrangements of the treatment and control: CCTT, TTCC, CTTC, TCCT, TCTC, and CTCT. Each block is randomly allocated to one of the six arrangements. This process is then repeated 10 times (as the number of blocks), until all 40 participants are assigned to all conditions.

This procedure is relatively straightforward and provides several advantages. It “forces” group size equality by guaranteeing that there is exactly 50–50 % assignment of treatment and control participants. Furthermore, the procedure controls for time-related biases as well: using six combinations masks the next assignment sequence and therefore avoiding, at least somewhat, the risk of selection bias (but not without reservations as soon discuss). Many find it quite elegant as well, and over the years, the PRBD has become very popular in clinical trials (Abou-El-Fotouh 1976; Cochran and Cox 1957; Rosenberger and Lachin 2002, p. 154). However, in criminology, this approach is quite rare (Ariel 2009).

Matched Pairs Design

A different yet related random allocation procedure is the pairwise matching assignment (see Rossi et al. 2006). Matched pairs, in which each member of the pair is assigned to either treatment or control conditions, can also be used to achieve maximum equivalence. The researcher is able to gain more statistical power from reduced variance rather than increased sample size. In this procedure, participants are often rank-ordered based on a particular variable (e.g., the number of previous arrests), and then every pair is randomly assigned to treatment or control conditions. Thus, the top two offenders would be assigned at random, one to the control group and the other to the experimental group, and then the third and fourth participants would be assigned in a similar way, then the fifth and the sixth, and so on until the last two cases. Each pair can be viewed as a “block”; in the example above, there are 20 blocks.

Matched pairs assignments are appealing, as they produce exactly the same group sizes. However, they do pose some threats. First, any interference with the “natural” randomization of case allocation can potentially introduce bias. Particularly in sequential assignments (i.e., a trickle flow process), knowing the allocation of the first case (“treatment”) immediately unmasks the assignment of the second case (“control”), and this can lead to selection bias. Second, by matching in pairs of ranked cases, one assumes that the “pairing criterion” (e.g., number of previous arrests) does not introduce a systematic bias to the procedure. Great caution should therefore be used when randomly assigning in pairs. Nevertheless, there can certainly be instances in which this design is a good fit. Hot-spot experiments can potentially benefit from this type of random allocation (e.g., Braga and Bond 2008).

A matched pairs design may also help to solve the problem of differential attrition. If one member of a matched pair drops out, the other member of the pair can be deleted as well, thus retaining the randomized design within matched pairs. For instance, in hot-spot experiments, it is conceivable that some “treatment hot spots” will have to be excluded after random assignment, if they are too far away from all other hot spots and difficult for the police to reach within reasonable time. In this case, the experimenter can drop the problematic “treatment hot spot,” along with the paired “control hot spot,” without jeopardizing the equivalence between the experimental and control groups. Nowadays, members of a pair can be matched on numerous variables by using propensity score matching (see, e.g., Apel and Sweeten 2010).

A Closer Look At The Blocking Criterion

Blocking on key variables is expected to create blocks of participants which are more similar to one another than in the generally heterogeneous random sample. In certain cases, it is immediately obvious that blocking should be utilized for the purposes of reducing experimental error resulting from variance. The advantage of blocking the data according to type of drug use, as in the hypothetical drug treatment trial presented above, is very clear. But there are other instances when the advantages of blocking are not as apparent.

Because the decision to block the data is usually based on qualitative grounds, there is always the risk that the researcher has made a poor decision. In an ordinal-level variable, for example, this means that the natural cutting points of the data might be misplaced, therefore implementing a grouping criterion that creates blocks in which the units within each block do not share common characteristics. In a study of tax evasion, for example, blocking the data according to income levels in a way that is intended to divide the sample into disparate socioeconomic backgrounds could go wrong if the researcher mistakenly categorized participants, so the blocks do not contain taxpayers with similar socioeconomic attributes. Thus, if the blocking is wrong, the block design will be disadvantageous compared with using an ordinary complete randomization design; such a procedure could actually be counterproductive and increase the error rate, because it increases the intra-block heterogeneity.

A practical approach to deal with this situation would be to ignore the blocking factor in analyses (Friedman et al. 1985). Disregarding the blocking effect is acceptable, because ignoring this factor should result in a more conservative statistical test. Analyzing the data this way will mean that the researcher sacrifices both power and precision, but not the overall integrity of the study, as long as the researcher implicitly reports this procedure.

Subgrouping Using Blocking Or Subgroup Analyses

The last issue to consider in regard to these designs is whether pre-random blocking is at all necessary. Randomized block designs decrease the variance of the data and increase the precision and statistical power of the test. This is achieved by the pre-randomization blocking procedure. However, ordinary post hoc subgroup analyses, which are generally used in analysis of variance procedures (such as Tukey’s HSD, Scheffe, Bonferroni, and the like), are used for exactly the same reason. These analyses allow the researcher to evaluate the treatment effect on particular groups or subgroups of participants. But in this context, they can also be used to theoretically homogenize the data according to certain key variables, much like a blocking procedure. Therefore, should data homogenization be dealt with before or after random assignment?

Subgroup analyses are customarily viewed as a natural step that comes after testing for main effects. These analyses can provide valuable information about both planned and unanticipated benefits and hazards of the intervention. At the very least, researchers use them to establish treatment benefits in subsets of participants. It makes sense to first assess the treatment by comparing all experimental units with all control units (or before–after, depending on the design) and then to account statistically for any covariates or other baseline variables. It seems that most clinicians agree with this rationale as 70 % of clinical trial reports include treatment outcome comparisons for participants subdivided by baseline characteristics at the postrandomization stage (Adams 1998; Assmann et al. 2000).

At the same time, however, as logical as subgroup analyses may be in theory, it is well established that they are often misleading. In fact, the medical community often rejects such findings (Moye and Deswal 2001), as the methods and procedures implemented are commonly misused (Assmann et al. 2000). Among some of the concerns raised against subgroup analyses, Moye and Deswal (2001) emphasize that “lack of prospective specification, inadequate sample size, inability to maintain power, and the cumulative effect of sampling error” complicate their interpretation. Some researchers go as far as saying that the most reliable estimate of the treatment effect for a particular subgroup is the overall effect rather than the observed effect in that particular group (Schulz and Grimes 2005). Therefore, using subgroup analysis instead of blocking the data before random assignment may actually be ill-advised.

Moreover, because virtually any covariate can be used to cluster units into subgroups, it allows, at least from a technical standpoint, the ability to generate multiple comparisons. This subgroup analysis is a source of concern, because it increases the probability of detecting differences simply by chance alone (type I error). It is not uncommon for researchers to be tempted to look for statistically significant, often publishable, differences between subgroups. It is therefore recommended that, without proper planning and sound rationale for conducting the analysis, subgroup analyses should not be considered as a replacement for pre-randomization blocking. Subgroup analyses should be justified on theoretical grounds a priori, in order to avoid the appearance of improper data mining. As described by Weisburd and Britt (2007, p. 320), “this is a bit like going fishing for a statistically significant result. However, sometimes one or another of the pairwise comparisons is of particular interest. Such an interest should be determined before you develop your analysis… if you do start off with a strong hypothesis for a pairwise comparison, it is acceptable to examine it, irrespective of the outcomes of the larger test. In such circumstances, it is also acceptable to use a simple two-sample t-test to examine group differences.” Schulz and Grimes (2005, p. 1658) further developed this argument, by emphasizing that “seeking positive subgroup effects (data-dredging), in the absence of overall effects, could fuel much of this activity. If enough subgroups are tested, false-positive results will arise by chance alone.. .. Similarly, in a trial with a clear overall effect, subgroup testing can produce false-negative results due to chance and lack of power.”

Thus, subgroup analyses can be misleading. The interpretation of their results should be seen as exploratory because they can suggest but not confirm a relationship in the population at large. Despite this recognition in other disciplines, most criminal justice experiments do not take multiple tests into account. It leads one to wonder how many of the findings from criminal justice experiments, in which hundreds of outcomes are reported, are really “true effects.”

Notwithstanding reservations just reviewed, subgroup analyses should not be completely neglected. There are times when they can replace pre-randomization blocking designs. This, however, should be done with caution. When the researcher specifies at the beginning of the trial (i.e., in the experimental protocol before “going live” with experiment) that the efficacy of the treatment for a particular subgroup or a particular block is of particular interest and part of the research goals, then subgroup analyses can be considered. When this is the case, there are good strategies that can be used to estimate the effect size in subgroups created after random assignment (see Moye and Deswal 2001). Practically, reporting the proposed analyzes in the experimental protocol can substantially reduce the “going fishing” bias described earlier.

Conclusions

Under certain conditions, randomized block designs are more useful than simple random allocation procedures. They allow the researcher flexibility and control over the number of conditions assigned to the participants, as well as the number of blocks that are used to homogenize the data. By reducing the intra-block variance, the treatment estimates are more accurate because of the increased statistical power and precision of the test statistics.

The various statistical models designed to accommodate the different types of blocking techniques provide the researcher with accuracy that is generally superior to that which can be obtained using simple random allocation. This is particularly the case when the trial is small – several hundred or less – or when the blocking criterion is “good.” These blocking procedures can deal with certain shortcomings that cannot be eliminated by randomization: increased data variance, outliers, time effects due to sequential assignment, missing data, and covariance imbalance. Blocking procedures can also create a more accurate estimate of the treatment effect – not by altering the effect of the treatment or the sample size, which are held constant, but by decreasing the variance. Therefore, given their clear advantages, these designs are gaining popularity in criminal justice research, and one should expect that they will be used more often in the future.

Bibliography:

Abou-El-Fotouh HA (1976) Relative efficiency of the randomized complete block design. Exp Agric 12:145–149
Adams K (1998) Post hoc subgroup analysis and the truth of a clinical trial. Am Heart J 136(5):753–758
Apel R, Sweeten G (2010) The impact of incarceration on employment during the transition to adulthood. Soc Probl 57:448–479
Ariel B (2009) Systematic review of baseline imbalances in randomized controlled trials in criminology. Presented at the communicating complex statistical evidence conference, University of Cambridge, UK
Ariel B (2012) Deterrence and moral persuasion effects on corporate tax compliance: findings from a randomized controlled trial. Criminology 50(1):27–69
Ariel B, Farrington D (2010) Randomised block designs. In: Weisburd D, Piquero A (eds) Handbook of quantitative criminology. Springer, New York
Armitage P (2003) Fisher, Bradford Hill, and randomization: a symposium. Int J Epidemiol 32:925–928
Assmann S, Pocock S, Enos L, Kasten L (2000) Subgroup analysis and other (mis)uses of baseline data in clinical trials. Lancet 355(9209):1064–1069
Braga A, Bond B (2008) Policing crime and disorder hotspots: a randomized controlled trial. Criminology 46(3):577–607
Braga A, Weisburd D, Waring E, Mazerolle LG, Spelman W, Gajewski F (1999) Problem-oriented policing in violent crime places: a randomized controlled experiment. Criminology 37:541–580
Chow S-C, Liu J-P (2004) Design and analysis of clinical trials: concepts and methodologies. Wiley-IEEE, Taiwan
Cochran WG, Cox GM (1957) Experimental designs. Wiley, New York
Friedman LM, Furberg CD, DeMets DL (1985) Fundamentals in clinical trials, 2nd edn. PSG, Littleton
Gill CE and Weisburd D (2013) Increasing equivalence in small sample place-based experiments: taking advantage of block randomization methods. In: Welsh BC, Braga AA, Bruinsma GJN (eds) Experimental criminology: prospects for advancing science and public policy. Cambridge University Press, New York
Weisburd D, Petrosino A, Mason G (1993) Design sensitivity in criminal justice experiments. Crime Justice 17(3):337–379
Weisburd D, Morris N, Ready J (2008) Risk-focused policing at places: an experimental evaluation. Justice Q 25(1):163–200
Hallstrom A, Davis K (1988) Imbalance in treatment assignments in stratified blocked randomization. Control Clin Trials 9(4):375–382
Hill AB (1951) The clinical trial. Br Med Bull 7:278–282
Kao L, Tyson J, Blakely M, Lally K (2007) Clinical research methodology I: introduction to randomized trials. J Am Coll Surg 206(2):361–369
Lachin JM (1988) Statistical properties of simple randomization in clinical trials. Control Clin Trials 9(289):312–326
Lipsey MW (1990) Design sensitivity: statistical power for experimental research. Sage, Newbury Park
Moye L, Deswal A (2001) Trials within trials: confirmatory subgroup analyses in controlled clinical experiments. Control Clin Trials 22(6):605–619
Rosenberger W, Lachin JM (2002) Randomization in clinical trials: theory and practice. Wiley, New York
Rossi P, Lipsey M, Freeman H (2006) Evaluation: a systematic approach, 7th edn. Sage, Newbury Park
Schulz KF, Grimes D (2005) Multiplicity in randomized trials II: subgroup and interim analyses. Lancet 365(9471):1657–1661
Torgerson JD, Torgerson CJ (2003) Avoiding bias in randomized controlled trials in educational research. Br J Educ Stud 51(1):36–45
Ttofi MM, Farrington DP (2012) Bullying prevention programs: the importance of peer intervention, disciplinary methods and age variations. J Exper Criminol
Weisburd D, Britt C (2007) Statistics in criminal justice. Springer, New York
Weisburd D, Green L (1995) Policing drug hot spots: the Jersey City DMA experiment. Justice Q 12:711–736
Weisburd D, Taxman FS (2000) Developing a multicenter randomized trial in criminology: the case of HIDTA. J Quant Criminol 16(3):315–340