This sample Specification Error Research Paper is published for educational and informational purposes only. If you need help writing your assignment, please use our research paper writing service and buy a paper on any topic at affordable price. Also check our tips on how to write a research paper, see the lists of research paper topics, and browse research paper examples.
In the context of a statistical model, specification error means that at least one of the key features or assumptions of the model is incorrect. In consequence, estimation of the model may yield results that are incorrect or misleading. Specification error can occur with any sort of statistical model, although some models and estimation methods are much less affected by it than others. Estimation methods that are unaffected by certain types of specification error are often said to be robust. For example, the sample median is a much more robust measure of central tendency than the sample mean because it is unaffected by the presence of extreme observations in the sample.
For concreteness, consider the case of the linear regression model. The simplest such model is
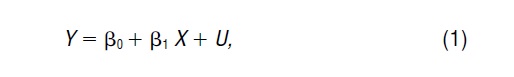where Y is the regressand, X is a single regressor, U is an error term, and ß0 and ß1 are parameters to be estimated.
This model, which is usually estimated by ordinary least squares, could be misspecified in a great many ways. Some forms of misspecification will result in misleading estimates of the parameters, and other forms will result in misleading confidence intervals and test statistics.
One common form of misspecification is caused by nonlinearity. According to the linear regression model (1), increasing the value of the regressor X by one unit always increases the expected value of the regressand Y by ß1 units. But perhaps the effect of X on Y depends on the level of X. If so, the model (1) is misspecified. A more general model is
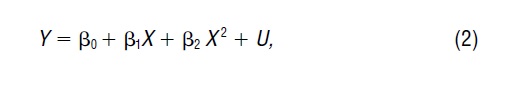
which includes the square of X as an additional regressor. In many cases, a model like (2) is much less likely to be misspecified than a model like (1). A classic example in economics is the relationship between years of experience in the labor market (X) and wages (Y). Whenever economists estimate such a relationship, they find that ß1 is positive and ß2 is negative.
If the relationship between X and Y really is nonlinear, and the sample contains a reasonable amount of information, then it is likely that the estimate of ß2 in (2) will
be significantly different from zero. Thus we can test for specification error in the linear model (1) by estimating the more general model (2) and testing the hypothesis that ß2 = 0.
Another type of specification error occurs when we mistakenly use the wrong regressor(s). For example, suppose that Yreally depends on Z, not on X. If X and Z are positively correlated, we may well get what appear to be reasonable results when we estimate regression (1). But the correct regression
should fit better than regression (1). A number of procedures exist for deciding whether equation (1), equation (3), or neither of them is correctly specified. These are often called nonnested hypothesis tests, and they are really a way of testing for specification error. In the case of (1) and (3), we simply need to estimate the model
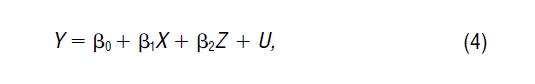
which includes both (1) and (3) as special cases. We can test whether (1) is correctly specified by using the t-statistic for ß2 = 0, and we can test whether (3) is correctly specified by using the t-statistic for ß1 = 0.
Of course, it is possible that Y actually depends on both X and Z, so that the true model is (4). In that case, if we mistakenly estimated equation (1), we would be guilty of omitting the explanatory variable Z. Unless X and Z happened to be uncorrelated, this would cause the estimate of ß1 to be biased. This type of bias is often called omitted variable bias, and it can be severe when the correlation between X and Z is high.
Another very damaging type of specification error occurs when the error term U is correlated with X. This can occur in a variety of circumstances, notably when X is measured with error or when equation (1) is just one equation from a system of simultaneous equations that determine X and Y jointly. Using ordinary least squares in this situation results in estimates of ß0 and ß1 that are biased and inconsistent. Because they are biased, the estimates are not centered around the true values. Moreover, because they are inconsistent, they actually converge to incorrect values of the parameters as the sample size gets larger.
The classic way of dealing with this type of specification error is to use instrumental variables (IV). This requires the investigator to find one or more variables that are correlated with X but not correlated with U, something that may or may not be easy to do. The IV estimator that results, which is also called two-stage least squares, is still biased, although generally much less so than ordinary least squares, but at least it is consistent. Thus, if the sample size is reasonably large and various other conditions are satisfied, IV estimates can be quite reliable.
Even if a regression model is correctly specified in the sense that the relationship between the regressand and the regressors is correct and the regressors are uncorrelated with the error terms, it may still suffer from specification error. For ordinary least squares estimates with the usual standard errors to yield valid inferences, it is essential that the error terms be uncorrelated and have constant variance. If these assumptions are violated, the parameter estimates may still be unbiased, but confidence intervals and test statistics will generally be incorrect.
When the error terms do not have constant variance, the model is said to suffer from heteroskedasticity. There are various way to deal with this problem. One of the simplest is just to use heteroskedasticity-robust standard errors instead of conventional standard errors. When the sample size is reasonably large, this generally allows us to obtain valid confidence intervals and test statistics.
If the error terms are correlated, confidence intervals and test statistics will generally be incorrect. This is most likely to occur with time-series data and with data where the observations fall naturally into groups, or clusters. In the latter case, it is often a good idea to use cluster-robust standard errors instead of conventional ones.
When using time-series data, one should always test for serial correlation, that is, correlation between error terms that are close together in time. If evidence of serial correlation is found, it is common, but not always wise, to employ an estimation method that “corrects” for it, and there are many such methods. The problem is that many types of specification error can produce the appearance of serial correlation. For example, if the true model were (4) but we mistakenly estimated (1), and the variable Z were serially correlated, it is likely that we would find evidence of serial correlation. The right thing to do in this case would be to estimate (4), not to estimate (1) using a method that corrects for serial correlation.
The subject of specification error in regression models and other statistical models has produced a vast body of research in statistics, econometrics, and other fields. A graduate-level textbook that covers this topic extensively is Econometric Theory and Methods (2004) by Russell Davidson and James MacKinnon. A less-advanced book that treats many of the same topics at a lower level is Jeffrey Wooldridge’s Introductory Econometrics (2006).
Bibliography:
- Davidson, Russell, and James G. MacKinnon. 2004. Econometric Theory and Methods. New York: Oxford University Press.
- Wooldridge, Jeffrey M. 2006. Introductory Econometrics: A Modern Approach. 3rd ed. Mason, OH: Thomson/South-Western.
See also:
Free research papers are not written to satisfy your specific instructions. You can use our professional writing services to buy a custom research paper on any topic and get your high quality paper at affordable price.
ORDER HIGH QUALITY CUSTOM PAPER
Always on-time
Plagiarism-Free
100% Confidentiality
