This sample Stochastic Frontier Analysis Research Paper is published for educational and informational purposes only. If you need help writing your assignment, please use our research paper writing service and buy a paper on any topic at affordable price. Also check our tips on how to write a research paper, see the lists of research paper topics, and browse research paper examples.
Stochastic frontier analysis (SFA) refers to a body of statistical analysis techniques used to estimate production or cost functions in economics, while explicitly accounting for the existence of firm inefficiency. The operative word in this definition is inefficiency, which implies producers may behave suboptimally in their decisions to maximize or minimize some objective function (e.g., profits, production, revenue, or costs). The intellectual underpinnings of inefficiency in economics can be traced to the writings of John Hicks (1938), who argued that monopolists possess motivations other than those of pure profit maximization; these motivations may lead to suboptimal production. (See Kumbhakar and Lovell [2000] for other rationalizations for inefficiency in equilibrium and a discussion of its intellectual underpinnings.)
The empirical departure point for SFA is the production frontier model, originally formulated by Aigner, Lovell, and Schmidt (1977) and Meeusen and van den Broeck (1977). Let
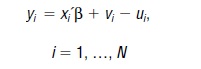
where firm i seeks to maximize production of observable output y., employing linear production function x’.f. Observable production inputs (e.g., labor and capital) are in column vector x. and marginal products are the corresponding column vector of unknown parameters, f. The v. is a zero-mean, symmetric error. The salient feature of the model is non-negative error, u. , representing unobserved inefficiency, so the specification is a leading case of an error-component model. The deterministic portion of the specification, xi ff, represents the frontier of maximal output for a given set of inputs x. . The symmetric error, v., causes the frontier to be stochastic. The one-sided inefficiency term, u. , can only reduce output and represents departure from this frontier.
If the inputs and outputs are in natural logarithms, then equation 1 is a Cobb-Douglas production function. Other common functional forms, such as the translog, can be modeled with appropriate selection of the components of x. . For example, a cost frontier can also be estimated if y. is total cost and x. are total output and input prices. Depending on the specification, u. can be technical (production), revenue, profit, or cost inefficiency.
Estimation of the parameters in equation 1 is complicated by the fact that the mean of inefficiency is nonzero, but either a modified ordinary least squares or a maximum likelihood algorithm are typically employed. For this particular specification, identification is achieved from an independence assumption onx. , v. , and u. and by specific distributional assumptions on the error components, such as v. normal and u. truncated normal, exponential, or gamma (Greene 1990). These assumptions may be difficult to justify. In particular, it has been argued that inefficiency is correlated with input mix and that specific distributions for the errors are too restrictive. Schmidt and Sickles (1984) relax these assumptions by considering panel data (firms observed over multiple time periods) and fixed-effect estimation, where inefficency is nonstochastic and time-invariant.
Methods for quantifying inefficiency itself are due to Jondrow et al. (1982), whereas Horrace and Schmidt (1996, 2000) develop methods from inference on inefficiency. Generalizations of the basic model are plentiful. Semi- and nonparametric estimation techniques have been considered (Fan, Li, and Weersink 1996). Time-varying inefficiency was first considered by Cornwell, Schmidt, and Sickles (1990) and Kumbhakar (1990). Applications are unlimited but include estimation of frontiers for industries in the manufacturing and services sectors, for government entities, and for samples of countries. There is also a complementary Bayesian estimation literature (van den Broeck et al. 1994). Finally, there is a competing, purely deterministic methodology called data envelopment analys.s, or DEA, developed by Charnes, Cooper, and Rhodes (1978).
Bibliography:
- Aigner, Dennis, C. A. Knox Lovell, and Peter Schmidt. 1997. Formulation and Estimation of Stochastic Frontier Production Function Models. Journal of Econometrics 6: 21–37.
- Charnes, Abraham, William W. Cooper, and Edwardo Rhodes. 1978. Measuring Efficiency of Decision-Making Units. European Journal of Operational Research 2: 429–444.
- Cornwell, Christopher, Peter Schmidt, and Robin Sickles. 1990. Production Frontiers with Cross-Sectional and Time-Series Variation in Efficiency Levels. Journal of Econometrics 46: 185–200.
- Fan, Yanqin, Qi Li, and Alfons Weersink. 1996. Semi-parametric Estimation of Stochastic Production Frontier Models. Journal of Business and Economic Statistics 14: 460–468.
- Greene, William. 1990. A Gamma Distributed Stochastic Frontier Model. Journal of Econometrics 46: 141–164. Hicks, John R. 1935. The Theory of Monopoly: A Survey. Econometrica 3: 1–20.
- Horrace, William C., and Peter Schmidt. 1996. Confidence Statements for Efficiency Estimates from Stochastic Frontier Models. Journal of Productivity Analysis 7: 257–282.
- Horrace, William C., and Peter Schmidt. 2000. Multiple Comparisons with the Best, with Economic Applications. Journal of Applied Econometrics 15: 1–26.
- Jondrow, James, C. A. Knox Lovell, Ivan S. Materov, and Peter Schmidt. 1982. On the Estimation of Technical Efficiency in the Stochastic Production Function Model. Journal of Econometrics 19: 233–238.
- Kumbhakar, Subal C. 1990. Production Frontiers, Panel Data, and Time-Varying Technical Inefficiency. Journal of Econometrics 46: 201–211.
- Kumbhakar, Subal C., and C. A. Knox Lovell. 2002. Stochastic Frontier Analysis. Cambridge, U.K.: Cambridge University Press.
- Meeusen, Wim, and Julien van den Broeck. 1977. Efficiency Estimation from Cobb-Douglas Production Functions with Composed Error. International Economic Review 18: 435–444.
- Schmidt, Peter, and Robin Sickles. 1984. Production Frontiers and Panel Data. Journal of Business and Economic Statistics 2: 367–374.
- Van den Broeck, Julien, Gary Koop, Jacek Osiewalski, and Mark F. J. Steel. 1994. Stochastic Frontier Models: A Bayesian Perspective. Journal of Econometrics 61: 273–303.
See also:
Free research papers are not written to satisfy your specific instructions. You can use our professional writing services to buy a custom research paper on any topic and get your high quality paper at affordable price.





