This sample Von Neumann-Morgenstern Utility Research Paper is published for educational and informational purposes only. If you need help writing your assignment, please use our research paper writing service and buy a paper on any topic at affordable price. Also check our tips on how to write a research paper, see the lists of research paper topics, and browse research paper examples.
Von Neumann—Morgenstern utility considers decision making under risk. It concerns choice when the probabilities of the possible outcomes of that choice are objectively known. This decision framework differs from decision making under certainty and decision making when probability is subjective. John von Neumann and Oskar Morgenstern (1947) follow a behavioral framework analogous to the revealed preference framework developed by Paul A. Samuelson (1938 and 1947). Quasi-operational experiments are envisioned where people’s behavior is held to satisfy key behavioral axioms.
The formal treatment of expected utility began with Daniel Bernoulli (1738) in his formulation of the St. Petersburg Paradox. In this paradox, a game is considered that has an infinite expected value. The paradox is that people will not pay a large sum to play this game. The game is one in which a fair coin (equal probability of a heads or tails) is tossed. If a head occurs the coin is tossed again and again until a tail occurs. Once a tail occurs the game is over. The payoff from playing the game depends on the number of consecutive heads that occurs. The payoff for H heads is defined as
That is, if one head occurs, $2 is paid; if two heads occur, $2 + $4 = $6 is paid; and so forth. The probability of at least one head is V2, the probability of at least two consecutive heads is J4, and so forth. Consequently, the expected value of the game is
Despite the infinite expected payoff, few would pay large sums to play this game. Bernoulli provided an answer to this paradox in terms of diminishing marginal utility. He argued that it is the utility of the gains and not the monetary gains from the game that are relevant to the person’s decision whether or not to play the game. With diminishing marginal utility, the gains from the game could be finite and small.
Von Neumann-Morgenstern utility can be illustrated by considering lotteries with two possible prizes, A and B, and a cost for playing the lottery, Y, with A < Y < B. Let P be the probability of the most favorable prize, B, and (1 – P) be the probability of the less favorable prize, A. Six key assumptions (Luce and Raiffa 1957) will assure that a utility function can be defined from the revealed preferences of players. These assumptions assure that a probability can be found for every lottery where the decision maker is indifferent between the price of the lottery ticket and the lottery. In other words,
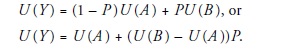
Suppose we rank every possible outcome of any lottery from W, the worst possible, to B, the best possible and assign an ordinal number to U (W) and U (B) representing this ranking. Then U (Y) for any Y can be found as a linear transformation of these two extreme outcomes. Hence, Von Neumann-Morgenstern utility is cardinal but only because it represents a linear transformation of the probabilities in the lotteries. It is not cardinal utility in any other context.
Bibliography:
- Bernoulli, Daniel. 1738. Specimen Theoriae Novae de Mensura Sortis. Trans. Louise Sommer in Exposition of a New Theory on the Measurement of Risk. Econometrica 22, no. 1 (January 1954): 23–36.
- Luce, R. Duncan, and Howard Raiffa. 1957 Games and Decisions. New York: Wiley.
- Samuelson, Paul A. 1938. A Note on the Pure Theory of Consumer’s Behavior. Economica 5: 61–71.
- Samuelson, Paul A. 1947. Foundations of Economic Analysis. Cambridge, MA: Harvard University Press.
See also:
Free research papers are not written to satisfy your specific instructions. You can use our professional writing services to buy a custom research paper on any topic and get your high quality paper at affordable price.
ORDER HIGH QUALITY CUSTOM PAPER
Always on-time
Plagiarism-Free
100% Confidentiality
