This sample Welfare Economics Research Paper is published for educational and informational purposes only. If you need help writing your assignment, please use our research paper writing service and buy a paper on any topic at affordable price. Also check our tips on how to write a research paper, see the lists of research paper topics, and browse research paper examples.
Welfare economics is a normative branch of economic theory that attempts to assess the implications of laws and institutions, including market outcomes, for human well-being. Welfare economics begins with John Stuart Mill’s “canons of taxation,” in which he applies rule-utilitarian ethics to suggest guidelines for taxation that might reduce its bad impacts. Nevertheless, A. C. Pigou’s Economics of Welfare (1920) can be thought of as the founding book of welfare economics. Among the propositions of welfare economics there would be a broad consensus, for example, that (1) in the absence of externalities, competitive equilibria are efficient, and (2) with few exceptions, taxes, monopoly power, and externalities tend to move the economy predictably away from an efficient allocation of resources.
The Utilitarianism Of Mill And Pigou
The ideas of Mill and Pigou are utilitarian in the narrow sense that they assume the following:
- Acts, laws, rules, and institutions should be evaluated on the basis of their consequences rather than on some intrinsic rightness or wrongness; that is, nothing is good unless it does somebody some good.
- Good and bad subjective states of mind are the consequences that should be considered in the assessment.
- For a particular individual, the degree to which good states of mind are attained, and bad states avoided, can be expressed by a number (called utility).
- Moreover, this number can be compared between individuals and cumulated over the population; and so this cumulative number can be made the objective of public policy.
This narrow utilitarianism would imply, among other things, that efficiency depends on the distribution of income as well as the allocation of resources. Many economists found this undesirable, on the grounds that one ought to be able to assess the efficiency of resource allocation apart from the distribution of income, as indeed Mill had suggested. This led them to reject the fourth assumption. For this purpose, Vilfredo Pareto had proposed the criterion that bears his name: An allocation of resources is said to be “Pareto optimal” if no one person can be made better off without making another person worse off. Without interpersonal comparability of utility, however, no discrimination can be made among Pareto optimal allocations as to which is better or worse.
Moreover, to some, the third assumption also seemed implausible. In place of numerical or “cardinal” utility, they held that individual decisions and well-being are based on a system of preferences. The “good states of mind” are the ones that the person prefers (which may not correspond to pleasure and pain), and therefore the vectors of consumption goods and services that produce the states of mind can be placed in an order from better to worse, from that individual’s point of view, but the ordering does not correspond to any unique numerical measure. As Paul A. Samuelson (1948) observes, however, the preferences could in principle be reconstructed from (“revealed” by) the observed choices of the individuals. The revision of welfare economics without the last two assumptions is known as the “new welfare economics.”
Indifference Curves
A preference system can be visualized by a map of “indifference curves.” Beginning from a particular vector of consumer goods, such as “one coffee and two doughnuts,” the indifference curve corresponding to that vector is the boundary between all of the vectors preferred to “one coffee and two doughnuts” and those to which “one coffee and two doughnuts” is preferred. If one assumes that this boundary is well-defined, it forms a curve with the property that, taking any two vectors along the curve, the individual feels no preference for one over the other. Thus, for example, if “one coffee and two doughnuts” and “two coffees and one doughnut” are on the same curve, then the individual can be said to be indifferent between the two, and accordingly the curve is called an indifference curve. The preference map can also be represented by any one of an infinite array of “utility indices,” provided that, comparing two consumption vectors, the higher number is assigned to the one that is preferred. In this case, however, the only valid conclusions of the analysis are those that do not depend on the specific utility index numbers used.
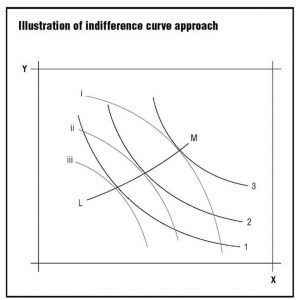
Francis Ysidro Edgeworth addressed the efficiency of allocation of goods in a pure exchange economy using the indifference curve approach (1995). First, assume that the total quantities available of two goods, good x and good y, are X and Y as shown in Figure 1. If the coordinates of a point in the interior of the diagram are x0, y0, then those are the quantities of the two goods allocated to individual j, and the quantities allocated to individual k are X — x0, Y — y0. Thus, the indifference curves for individual j are oriented to the x, y axis and are shown by curves 1, 2, 3, while the indifference curves for individual k are inverted and are illustrated by curves i, ii, iii. The points of tan-gency of two indifference curves, shown by the contract curve LM, are all Pareto optimal allocations of the two goods between the two individuals. In general, then, there will be infinitely many Pareto optima. A shift from one Pareto optimum to another trades off one person’s preferences against those of the other person.
To visualize this trade-off, one assigns a numerical index u to each indifference curve 1, 2, 3 and a numerical index uk to each indifference curve i, ii, iii. One must keep in mind that these arbitrary indices of utility cannot be compared as between the two individuals nor added. Figure 2 shows a diagram with uj on the horizontal axis and uk on the vertical axis. Any combination of utility indices (indifference curves) on or beneath this curve are attainable when X and Y are produced, while none of the combinations beyond the curve are attainable. This is called the constrained utility possibility frontier corresponding to the production of X and Y.
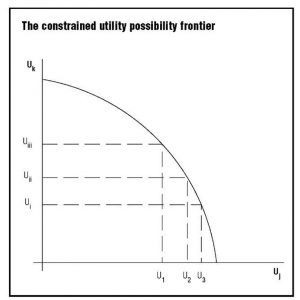
Suppose one carries out the same exercise for each technically efficient, feasible set of outputs X, Y. One would then trace the outer limit of all of the constrained utility possibility frontiers obtained in this way. This outer limit is the grand utility possibility frontier or simply the utility possibility frontier. With an appropriate change in the definitions of u1, u2, … u…, one may take Figure 2 as illustrative of the utility possibility frontier. Every point on this frontier has the properties that (1) the two goods produced are allocated between the two persons in a Pareto optimal way; and (2) production is technically efficient—that is, no reallocation of resources can increase the production of one good without reducing the production of the other; and (3) therefore, production and allocation is Pareto optimal over all possible allocations of resources and consumer goods. With appropriate mathematical notation, this conception can be extended to very large numbers of distinct goods and services and a very large population of agents.
Selecting Allocations
Two issues remain in this analysis. First, how does one choose the “best” among the points on the frontier? Second, for many practical problems, one must choose between two allocations, at least one of which is not Pareto optimal. How may one do that?
Taking these questions in reverse order, the new welfare economics answers the second question with a cost—benefit analysis based on the “Kaldor-Hicks compensation test,” named after Nicholas Kaldor (1939) and John R. Hicks (1939). One may illustrate this compensation test with an example of property on the banks of a river. John Doe owns land on the banks of Flowing River, while Richard Roe owns downstream property, including both banks. Roe builds a dam, entirely on his own property. The impoundment of Flowing River floods Doe’s property. In this sequence, Roe is the gainer and Doe the loser in clear senses. But can one say that Roe’s benefits exceed Doe’s costs?
To answer this question, one considers whether Roe could allocate some of his benefits to compensate Doe and still be a gainer on net? This is the Kaldor-Hicks test, and if the answer is yes, then building the dam is a potential Pareto improvement. That is, if the dam is built, there is a distribution of income that would leave everyone in society better off than they were without the dam. But another, equally reasonable, compensation test asks: Could Doe compensate Roe for ceasing and desisting from dam building, so that Roe would be better off than he would be if the dam were built? This is the Scitovszky test—named after Tibor de Scitovszky (1941)—and if the answer is yes, the world without a dam is potentially Pareto superior to the world with the dam. The two tests would be equivalent if benefits and costs were independent of the distribution of wealth, but, as Hicks noted,they are not. If the dam is built, and compensation is not paid, then wealth is redistributed and a new situation created. From the new situation, it might be a potential Pareto improvement to return to the original position. In practice, there is likely to be little difference between the two, because the impacts of the shifting income distribution is likely to be small relative to the impact of a project, and the Kaldor-Hicks test is the one usually used.
The Social Welfare Function
Is it possible, then, to choose one among the allocations on the utility possibility frontier that is the optimum of optima? For example, some might prefer an allocation with a more equal distribution of income or one in which certain “basic needs” are more thoroughly met, or that satisfy other conditions. Ideally, one might hope to express some consensus of such conditions in a social welfare function that would indicate which allocations are socially preferable to other allocations independently of their technical feasibility. Visualizing this social welfare function as a set of social indifference curves, and superimposing it on the grand utility possibility frontier, results in Figure 3. In this figure, the grand optimum allocation of resources could be identified with point V Further, following Samuelson (1956), the utility index could be made an index of real income. Remember that any numbers that correspond to indifference curves and assign larger numbers to the more highly preferred curves can be used as utility index numbers. In general, an index of real income will have this property. Therefore, suppose the axes measure the real incomes, R. and R, , of the two individuals.
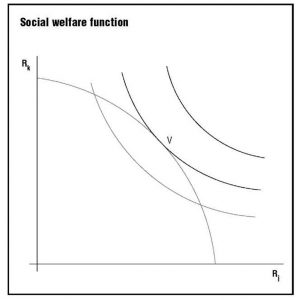
With this interpretation, the curvature of the social indifference curves could express one’s attitudes toward income equality, so that, for example, social indifference curves tightly curved around the 45-degree line would express a strong preference for equal incomes.
This ideal was set back by the Nobel laureate research of Kenneth J. Arrow (1951), in his general (im)possibility theorem. Arrow showed that, if we require some reasonable-seeming conditions on the social welfare function, such as the requirement that it generate transitive preferences, there could be no social welfare function that would satisfy them all. For a system of majority rule, for example, Arrow adapted a paradox attributed to the marquis de Condorcet (1972) to show that (imposing his other conditions) voting outcomes could always be cyclical rather than transitive. But Arrow also extended this to any (nonmajoritarian) social welfare rule, and in the context of his theorem, it is equally impossible to say that a market outcome defines a social welfare optimum.
Arrow’s theorem has spawned a large literature of reconsideration. Sometimes the conditions he proposed for a social welfare function can seem less self-evidently appropriate on further consideration. For example, one of the conditions is “nondictatorship,” mathematically expressed; but in some simple models of majority rule, the median person is a “dictator” in Arrow’s mathematical sense, although not on a conventional understanding of dictatorship. Thus, much of the controversy has centered on the refinement of Arrow’s conditions, and there is a large variety of possibility and impossibility theorems. All the same, Arrow’s discussion raised enough doubts about the concept of a social welfare function that it has been little used since the mid-twentieth century.
New Utilitarian Approaches
The new welfare economics is utilitarian only in the broader sense in that it accepts assumptions (1) and (2) above. But the narrower utilitarian approach is not dead. Game and decision theorists reformulated utility theory so that an objective numerical measure of utility can be based on observations of risk-averse behavior. In social philosophy, John Rawls (1971) renewed the social-contract theory, arguing that public policy should promote the interests of the least-favored individual. One interpretation of this is that it demands interpersonal comparison of utility and supplies a social welfare function based on the minimax principle. Drawing on the reformulation of utility theory and Rawls’s social-contract approach, John C. Harsanyi (1975) argued that social welfare could after all be based on a summation of individual utilities. Like Harsanyi, Amartya Sen (1985) admits interpersonally comparable utilities, at least as a logical possibility, and he has proposed conditions less limiting than Arrow’s that allow the possibility of a consistent majoritarian social welfare function. Sen, however, rejects what he describes as the welfarism of both the old and the new welfare economics, by which he means the supposition that the goodness of a social system depends only on the welfares of individuals in those social systems. In addition, Sen would have data on the capacities and perhaps freedoms of individuals reflected in the normative evaluation of economic society.
For many welfare economists, inequality in the income distribution is something to be avoided, but that cannot be completely avoided because of the sacrifice of production that would result. But inequality is not a simple thing in itself. Anthony Atkinson has made important contributions to the measurement of inequality and incorporation of inequality in discussions of policy issues such as taxation and fiscal policy. In 2001, Atkinson addressed “The Strange Disappearance of Welfare Economics.” Atkinson does not suggest that welfare judgments are disappearing from economics. Quite the contrary. For Atkinson, “welfare economics” comprises systematic and critical thinking in normative economics, and he notes with regret the de-emphasis of welfare economics from graduate programs and from the current research literature. The result, he suggests, is a proliferation of ill-considered value judgments in economic research, including a good deal of prejudice and confusion. Atkinson illustrates this with examples from recent macroeconomics, a field which perhaps has never been rich in careful thinking on value issues. For Atkinson, then, welfare economics has never been more needed, although this field of study receives far less attention than it did two generations ago. On the whole, nevertheless, welfare economics is a highly developed branch of economic theory that supplies tools for applications in cost—benefit analysis, but that also raises unsettled questions for future research.
Bibliography:
- Arrow, Kenneth J. 1951. Social Choice and Individual Values. New York: Wiley.
- Atkinson, Anthony B. 2001. The Strange Disappearance of Welfare Economics. Kyklos 54 (2/3): 193–206.
- Condorcet, Marie-Jean-Antoine-Nicolas de Caritat, Marquis de. 1972. Essai sur l’application de l’analyse a la probabilite des ecisions rendues a la pluralite des voix [Essay on the application of analysis to the probability of majority decisions]. New York: Chelsea Publishing. (Orig. pub. 1785.)
- Edgeworth, Francis Ysidro. 1995. Mathematical Psychics. Mountain Center, CA: James and Gordon. (Orig. pub. 1881.)
- Harsanyi, John C. 1975. Can the Maxim in Principle Serve as a Basis for Morality? A Critique of John Rawls’s Theory. American Political Science Review 69 (2): 594–606.
- Hicks, John R. 1939. Foundations of Welfare Economics. Economic Journal 49 (196): 696–712.
- Kaldor, Nicholas. 1939. Welfare Propositions of Economics and Interpersonal Comparisons of Utility. Economic Journal 49 (195): 549–552.
- Mill, John Stuart. 1987. Principles of Political Economy. Ed. William Ashley. Fairfield, NJ: A. M. Kelley. (Orig. pub. 1909.)
- Pareto, Vilfredo. 1971. Manual of Political Economy. Trans. Ann S. Schwier. Eds. Ann S. Schwier and Alfred N. Page. New York: A. M. Kelley. (Orig. pub. 1906.)
- Pigou, A. C. 1920. The Economics of Welfare. London: Macmillan.
- Rawls, John. 1971. A Theory of Justice. Cambridge, MA: Harvard University Press, Belknap Press.
- Samuelson, Paul A. 1948. Consumption Theory in Terms of Revealed Preferences. Economica 15 (60): 243–253.
- Samuelson, Paul A. 1956. Social Indifference Curves. Quarterly Journal of Economics 70 (1): 1–22.
- Scitovszky, Tibor de. 1941. A Note on Welfare Propositions in Economics. Review of Economic Studies 9 (1): 77–88.
- Sen, Amartya. 1985. Commodities and Capabilities. Amsterdam: North-Holland.
See also:
Free research papers are not written to satisfy your specific instructions. You can use our professional writing services to buy a custom research paper on any topic and get your high quality paper at affordable price.






