This sample Yield Research Paper is published for educational and informational purposes only. If you need help writing your assignment, please use our research paper writing service and buy a paper on any topic at affordable price. Also check our tips on how to write a research paper, see the lists of research paper topics, and browse research paper examples.
In economics and finance the word yield is used to describe the interest rate on a bond. In fact, the words yield and interest rate are used interchangeably and mean the same thing. There are several ways of calculating interest rates, with the most important being the yield to maturity, also known in many contexts as the internal rate of return. Economists consider the yield to maturity as the most accurate measure of the interest rate, and this is what they have in mind when they talk about interest rates.
The yield to maturity is the interest rate that equates the present value of payments received from a debt instrument with its cost (its value today). As an example, consider a simple, one-year loan. Assuming that you borrowed $1,000 for a year and you are required to repay the principal of $1,000 one year from now along with an interest payment of $100, then (according to the definition) the yield to maturity is given by
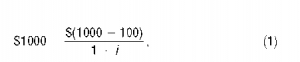
where $1,000 is the value of the loan today and $(1,000 + 100)/(1 + i) is the present value of the payments received from this instrument. Solving equation (1) for i yields i = 0.10 (or 10%). In this case, the yield to maturity is the same as the simple interest rate, the latter being calculated as the ratio of the interest payment to the principal, $100/$1,000.
Although for simple loans, the yield to maturity equals the simple interest rate, this is not the case for other debt instruments. To calculate the yield to maturity on an n-year coupon bond with market price P, coupon payment C, and face value F, the following formula is used (see Mishkin and Serletis 2007, Chapter 4, for more details):
![]()
If P, C, F, and n are all known, then the above equation could be solved for the yield to maturity on the n-year bond (also known as the n-year interest rate), i. It should be noted that the yield to maturity is different from the coupon rate of interest, the latter being the ratio of the yearly coupon payment to the bond’s face value, C /F. In fact, when the coupon bond sells at its face value (P = F), the yield to maturity is the same as the coupon rate; when the bond sells at a discount from face value (P < F), the yield to maturity is greater than the coupon rate; and when the bond sells at a premium from face value (P> F), the yield to maturity is less than the coupon rate. Equation (2) also shows that the yield to maturity and the price of a coupon bond are negatively related; when the yield to maturity increases, the price of the coupon bond falls, and when the yield to maturity falls, the price of the coupon bond rises.
As already noted, the yield to maturity can be calculated by solving equation (2) for i, if P, C, F, and n are known. But this equation is difficult to solve algebraically, especially for high values of n. However, the same answer can be obtained using a financial calculator. Consider, for example, an eight-year, 10 percent coupon bond, with a face value of $1,000, selling for $900. Set a Texas Instruments BA-35 solar calculator in FIN mode by pressing the MODE key until the word FIN appears on the screen, and clear it by pushing the 2nd key and then the CE/C key. To find the yield to maturity:
- Enter 900 and push the PV key.
- Enter 1000 and push the FV key.
- Enter 8 and push the N key.
- Enter 100 and push the PMT key.
- Push the CPT key and then the %i key.
The answer is 12.01 (or 12.01%).
Because of difficulties in calculating the yield to maturity, other less accurate measures of the interest rate have also come into common use in economic and finance. Two such measures are the current yield and the yield on a discount basis. The current yield is calculated as the ratio of the bond’s yearly coupon payment, C , to the bond’s current market price, P. That is,
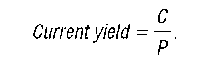
The current yield is the best approximation to the yield to maturity for coupon bonds, and changes in the current yield always signal changes in the same direction for the yield to maturity.
In the case of discount bonds, the interest rate is usually quoted as a yield on a discount basis. Discount bonds are bonds that sell at a discount from face value and involve no periodic coupon payments (this is why they are also known as zero-coupon bonds). Treasury bills and long-term zero-coupon bonds are examples of discount bonds. Consider, for example, a ninety-day Treasury bill with a face value F selling at a price P. The yield on a discount basis (also known as discount yield) is usually calculated as follows:
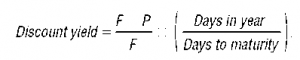
A related concept is the yield curve. The yield curve, published in the financial pages of most newspapers, shows the yield to maturity, i, as a function of the term to maturity, n. When the yield curve is upward sloping (the most typical case), the yield to maturity on long-term bonds (or, equivalently, the long-term interest rate) is greater than the yield to maturity on short-term bonds (the short-term interest rate); when the yield curve is downward sloping (referred to as an inverted yield curve), the spread between long- and short-term interest rates is negative; and when the yield curve is flat, short- and long-term interest rates are the same.
Early investigations into the yield curve looked at whether the slope of the yield curve can help predict future short-term interest rates and the level of economic activity. It was found that the yield curve does not always help predict future short-term interest rates—see, for example, Shiller, Campbell, and Schoenholtz (1983) and Mankiw and Summers (1984). More recent research based on better testing procedures, however, supports the view that the slope of the yield curve contains useful information about future interest rates over the short run and the long run, but not over the intermediate term—see, for example, Fama (1984) and Campbell and Shiller (1991). Moreover, research over the past twenty-five years has documented a relationship between the slope of the yield curve and the overall level of economic activity; it has been shown that the slope of the yield curve is a good predictor of future economic activity. More recently, Estrella and Trubin (2006) offer practical guidance regarding the use of the yield curve as a forecasting tool in real time.
Bibliography:
- Campbell, John Y., and Robert J. Shiller. 1991. Yield Spreads and Interest Rate Movements: A Bird’s Eye View. Review of Economic Studies 58: 495–514.
- Estrella, Arturo, and Mary R. Trubin. 2006. The Yield Curve as a Leading Indicator: Some Practical Issues. Federal Reserve Bank of New York. Current Issues in Economics and Finance 12 (July/August): 1–7.
- Fama, Eugene. 1984. The Information in the Term Structure. Journal of Financial Economics 13 (4): 509–528.
- Mankiw, N. Gregory, and Lawrence H. Summers. 1984. Do Long-Term Interest Rates Overreact to Short-Term Interest Rates? Brookings Papers on Economic Activity 1: 223–242.
- Mishkin, Frederic S., and Apostolos Serletis. 2007. The Economics of Money, Banking, and Financial Markets, 3rd Canadian ed. Toronto: Addison Wesley.
- Shiller, Robert J., John Y. Campbell, and Kermit L. Schoenholtz. 1983. Forward Rates and Future Policy: Interpreting the Term Structure of Interest Rates. Brookings Papers on Economic Activity 1: 173–217.
See also:
Free research papers are not written to satisfy your specific instructions. You can use our professional writing services to buy a custom research paper on any topic and get your high quality paper at affordable price.





