Experimental Designs Research Paper

This sample Experimental Designs Research Paper is published for educational and informational purposes only. If you need help writing your assignment, please use our research paper writing service and buy a paper on any topic at affordable price. Also check our tips on how to write a research paper, see the lists of psychology research paper topics, and browse research paper examples.

Knowing about experimental designs is essential if you are planning an experiment. It is highly unlikely that you would decide to set off on a cross-country trip without a road map. Although you might eventually reach your destination, you would likely waste time and money getting there. On the other hand, you might get hopelessly lost and never find your planned stopping point. Likewise, you should never plan an experiment without first considering its design. Although you might be fortunate and plan an experiment that would answer the question that you had in mind, it is much more likely that you would waste your time and end up with a mess on your hands.

Purpose Of Experimental Designs

Psychologists use experiments to answer questions about behavior. As a student of psychology, you probably have had many such questions yourself (e.g., why did that person act in that way?). Without research, we are left with no way to answer such questions except by guessing. A well-designed experiment, however, can put us on the road to answering a causation question more definitively. The question of causation is an elusive one, but one that scientists seek to answer.

A researcher typically begins with a hypothesis about the cause of a particular behavior. A hypothesis is some-what like an educated guess—based on results from previous research and observations of behavior, a researcher generates a hypothesis about the cause(s) of a behavior or a factor that will affect that behavior. The researcher uses that hypothesized cause or factor as an independent variable (IV) in the experiment. An IV is the variable whose effects you wish to study in your experiment. Of course, to determine the effects of an IV, you must have something with which to measure those effects—in our case, it would be the behavior that the researcher believes the IV will affect. This behavior or outcome variable is known as the dependent variable (DV). So, a researcher plans an experiment to determine the effect of an IV on a DV, which sounds relatively simple. However, complicating this process is another category of variables—extraneous variables. Extraneous variables are variables besides the IV that might have an effect on the behavior in question (the DV). There are probably few, if any, behaviors that are so simple that there is only one causative factor or variable. Thus, when we conduct an experiment, we must take steps to ensure that we are studying only the effect of our IV on the DV and not the effect of any extraneous variable(s). Experimental design is a helpful tool for the researcher in the quest to answer questions of causation in an experiment.

Fortunately, learning about experimental designs is easier than most students think it will be. Once you know a few basics about research and experiments, you can plan an experiment and choose the correct design for it simply by answering a series of questions (see Table 9.1).

Table 9.1 Outline of decisions to choose an experimental design

Independent Variables

As you can see in Table 9.1, the first question you must answer is “How many independent variables does your experiment have?” For example, suppose people have told you all your life about how important sleep is to good academic performance; thus, you would like to conduct an experiment to investigate the effects of sleep, in particular the notion of “adequate sleep.” Sleep would be your IV, so you have only one IV in your experiment. However, your choice of IV should immediately bring to mind some questions about what constitutes adequate sleep. This situation is often the case when you plan an experiment—the IV is somewhat vague, so you must develop an operational definition for the IV. It is important to develop a good, reliable operational definition so that people who read about your experiment will understand what you meant by your IV and could conduct their own experiment using your IV.

Operational Definition

An operational definition is one that entails what you, as the experimenter, have done to cause the IV to occur. As you think about the term “adequate sleep,” you can probably think of many different ways to define that term. As the experimenter, you control and are responsible for the way that you define the IV. For example, is adequate sleep six hours of sleep a day? Is it eight hours of sleep a day? Does adequate sleep mean more than simply a certain number of hours of sleep a day? As you can see, deriving an operational definition of your IV of adequate sleep will require some work on your part. Lest you decide that adequate sleep is a bad choice for an IV because it may be difficult to operationally define, you should realize that many potential IVs have similar problems with definitions. Think, for example, about such IVs as hunger, music, therapy, motivation, and so on—all would require a precise operational definition for use in an experiment, just as “adequate sleep” would. Let’s assume that you choose to define adequate sleep as eight hours of sleep a day—a fairly standard recommendation that you can find on sleep Web sites and in popular press articles. You now have your IV and its operational definition—at least for one group.

Comparison Group

Typically, you, as the experimenter, must also develop an operational definition for a comparison group within your IV. If you wish to study the effects of adequate sleep, you must compare participants who get adequate sleep to some other group (or groups) of participants. Given your interest in adequate sleep, you will probably want to compare your participants to other participants with less-than-adequate sleep (or typical sleep)—but how do you define “less-than-adequate sleep”? As you can probably imagine, you should develop the operational definition of your comparison group relative to the operational definition of your experimental group. Because of much recent evidence about the sleep habits of college students (e.g., http://www.cbsnews. com/stories/2004/04/19/health/main612476.shtml), let’s say that you define less-than-adequate sleep as six hours of sleep per night. Just as with the IV, you have a choice of how to define your comparison group.

At this point, students often get confused and decide that they have two IVs: adequate sleep and less-than-adequate sleep. Actually, you simply have one IV (sleep) with two groups or levels (adequate and less-than-adequate) of that IV. As you can tell from examining Table 1, it is critical that you can tell that this example has only one IV. Be sure not to confuse IVs with levels of an IV. Levels of an IV are simply the comparison groups of different values (or types) of the same IV.

Measuring the Effect of the IV

When you use an IV in an experiment, you must decide how to measure its effect—in other words, you musthave a “yardstick” of some sort to measure whether the IV affected something. For example, in our hypothetical example, you must decide how you would like to assess the effect(s) of adequate and less-than-adequate sleep. Although sleep is the variable of interest to you, you must also have another variable of interest to gauge the effect of sleep. This variable will be your DV. It will be necessary for you to develop an operational definition for your DV, just as you did for the IV. As you can imagine, the DV should be some variable that you can reasonably assume would show the effect of the IV. It would be silly, for instance, to say that you wanted to measure the effect of sleep on eye color—there is no logical link between those two variables. Given that you will probably be conducting an experiment over a short period of time, the DV should be something that sleep might affect over that short duration. Although sleep might affect people’s physical health, for example, those effects might take months to achieve. To measure the shorter-term effects of sleep, you decide to give your experimental participants an exam after getting either adequate or less-than-adequate sleep for a full week. After reading that sentence, you may have thought that the experimenter would need to specify an exact exam in order to meet the requirement of an operational definition. If this thought occurred to you, congratulations!

Manipulated Versus Measured IVs

You must also decide how you will present, administer, or measure the IV. As the experimenter, you have the opportunity to be in control of the IV—at least in many cases. If you can actually cause the IV to occur, then you can manipulate the IV. A manipulated IV is your better choice, as you will see. Using your IV in the hypothetical experiment we have been discussing, you could manipulate adequate sleep by controlling how long your participants sleep. You might need to provide them with a location to sleep—perhaps by giving them a bed in a sleep laboratory or some facility where you could monitor how long they sleep. This approach would be more work for you than allowing participants to monitor their own sleep, but it would provide you with more control. On the other hand, sleep also could be a measured IV. Rather than actually causing the IV to occur, you could measure the IV in your participants. If you had your participants report their sleeping habits to you, you could measure or classify them as to whether their sleep was adequate or not. Given your operational definition of adequate sleep, however, it might be difficult to find many participants who meet that precise definition. Also, people might not remember exactly how long they slept and simply provide you with their best guess. As you can see, by measuring or classifying your IV, you lose a good bit of control over the situation.

Why would you, as an experimenter, want to measure or classify an IV rather than manipulating it? One potential advantage is that measuring or classifying is often a simpler process. Asking participants about their sleep is far easier than actually manipulating it. But, in the case of adequate sleep, you could use either a manipulated or a measured IV. The main reason for measuring or classifying an IV rather than manipulating it, however, is that some IVs simply cannot be manipulated. Suppose you wanted to deal with personality type as an IV. There is no way to cause participants to possess a certain personality; instead, you could only measure personality type and assign participants to groups based on what you measured. Thus, when you choose your IV, you will have to decide whether you can manipulate it or whether you will have to measure or classify it; in some instances, you may have a choice. Let’s see why you would want to manipulate your IV, if possible.

Advantage of IV Manipulation

In an ideal world, an experiment is a tightly controlled situation in which the experimenter has total control (or nearly so) over all variables in the environment. Having control allows the experimenter to manipulate the IV, which means that any participant could be a part of any group. Thus, any participant could be in the adequate sleep group or the less-than-adequate sleep group because the experimenter controls the participants’ sleep. Having control also allows the experimenter to hold other factors in the experiment constant, so that they do not change unless the experimenter wants them to change. Being able to control and manipulate the IV, as well as other variables in the environment, has a major benefit over measuring or classifying the IV: You can attribute causality to the IV. Causality (also known as “cause and effect”) allows you to conclude that the IV has actually had an effect.

When you simply classify your IV, you lose the ability to make cause-and-effect statements. If you simply allow experimental participants to report their levels of sleep, you still are able to classify them as getting adequate or less-than-adequate sleep. However, it is possible that an extraneous variable will also become a factor in your research. Imagine, for example, that most of the students who report adequate sleep are freshmen and sophomores, whereas those reporting less-than-adequate sleep are mostly juniors and seniors. In this case, you would have an extraneous variable changing at the same time as your measured IV. Thus, your research would be confounded, which means that you cannot discern the causative variable if your two groups perform differently on the test. It could be sleep differences that led to differing scores, but it could also be classification differences that influenced the scores—you simply cannot tell. On the other hand, if you actually manipulate and control participants’ sleep, then you could have classifications spread evenly between your two groups, thus removing classification as a potential extraneous variable. In this manner, you still can draw a causative conclusion about the effects of differing amounts of sleep on exam scores.

Number Of Groups/Levels

Table 9.1 shows that, with one IV, the second major question to ask is “How many groups or levels does your IV have?” As we have already seen, there must be a comparison group that you use to gauge whether your IV has had an effect. If you simply administered your IV to a group of participants and had no group with which to compare them, you would not actually have an experiment. There would simply be no way to determine whether your IV affected behavior in that situation. Thus, the simplest possible experiment has one IV with two groups.

One-IV/Two-Group Experimental Design

This design description specifies the simplest possible experimental design. There is only one IV, with two groups (see Figure 9.1 for a concrete example)—typically, as noted earlier, both a group that experiences the IV and a comparison group; however, there could simply be two comparison groups. To elaborate, there are two typical approaches that experimenters take to using a comparison group. The first approach is to use a control group—a group that does not receive the IV. Thus, if you were interested in the effects of an afterschool tutoring program, the control group would not receive afterschool tutoring, whereas the experimental group would receive the tutoring. The experimental group is simply the group of participants that receives the IV. The second approach to making a comparison group is to give both groups the IV, but in differing amounts or types. In our current example, going without sleep for a week is not possible, so you could not use a presence/absence manipulation. Thus, we must use this second approach and vary the amount of sleep: 8 hours versus 6 hours. Likewise, if you were conducting a drug study, you could vary the amount of the drug: 5 versus 10 milligrams, for example. On the other hand, if you were studying different therapeutic approaches to depression, you would want to compare different types of therapy.

Researchers often use the first approach mentioned in the previous paragraph early in their research with a particular IV—the presence/absence manipulation makes it relatively easy to determine whether the IV has an effect. After researchers know that an IV does have an effect, they can then use the second approach to determine more particular details about the IV’s effects (e.g., Does the IV have an effect at low levels? Does one type of IV have a stronger effect than another?). Neither of the two approaches is particularly better than the other one; the specific IV may make the presence/absence manipulation impossible, or the particular research question may dictate one approach over the other. Again, given the particular IV in our example (sleep), we will be using the second approach (varying the amount of IV) from this point on.

Figure 9.1 Outline of decisions to choose an experimental design.

Assignment Of Participants To Groups

The final question that we need to answer (see Table 9.1) revolves around how we form groups of participants. The simplest possible method is to randomly assign the participants to the two groups. Random assignment means that all participants have an equal chance of being assigned to either group. It should be obvious to you that random assignment indicates a manipulated IV rather than a measured IV—if the IV was measured or classified, participants are essentially preassigned to their groups based on the groups (levels) of the IV. When experimenters use random assignment, the resulting groups are called random groups, which means that participants in one group have no relationship to participants in the other group. Because both groups are formed randomly, statistically, they should be equal. For example, if you had 40 students serving as your participants and randomly assigned them to two groups of 20, those two groups should be equated on a variety of variables such as intelligence, personality, motivation, and so on. Beginning with groups that are equal is critical to determining causality attributed to the IV. When an experiment begins with equal groups, and the experimenter treats the two groups identically (control) except for the variation of the IV, then any difference in the groups at the end of the experiment must be due to the manipulated IV. As you can see from Table 9.1, when you have one IV with two groups and assign participants to the groups randomly, you have an experimental design known as a two independent groups design. The “two groups” phrase signifies one IV with two groups, and the term “independent” indicates that the two groups have participants assigned randomly (which makes the groups independent of each other).

Sometimes experimenters worry that random assignment will not result in equal groups. Perhaps the number of participants is quite small, so that random assignment is somewhat less reliable, or maybe the researcher fears unknown variables that might not be equated through random assignment. In such a case, experimenters may choose a nonrandom method of assigning participants to groups so that equality of groups is more certain. There are three such nonrandom methods, all of which result in a relationship between participants in the groups such that they are not independent groups.

In matched pairs designs, experimenters measure their participants on some relevant variable (e.g., intelligence for a learning experiment) and then create pairs of participants who are equated on that variable. Thus, as far as the relevant variable is concerned, the participants are the same (i.e., they have the same level of intelligence). For this reason, we speak of a correlation existing between each set of two participants. If we know that age is an important variable in sleep research, then we may want to pair our participants in terms of age—have two 18-year-olds, two 30-year-olds, and so on paired together.
In repeated measures designs, experimenters measure their participants more than once—under each condition of the IV. For example, in our example using sleep as the IV, each participant would take part in the experiment in both the adequate and less-than-adequate sleep groups (obviously not at the same time)—in essence, each participant serves as his or her own control. Each participant would sleep eight hours a night for some number of days and then experience the DV measurement. The participants would then do the same thing a second time, except for sleeping six hours a night. To prevent the order of treatments from becoming an important factor in the experiment, the experimenter would exert control over the situation and counterbalance the treatments. In this example, counterbalancing means that half of the participants would sleep eight hours a night first, followed by the six hours a night condition. The other half of the participants would get their nights of six- and eight-hour sleep in the opposite order. Thus, the experimenter would have counterbalanced the order of treatments so that any effects of the order would essentially be negated (or cancelled out).

Repeated measures design is a popular method of creating correlated groups for several reasons: (a) it reduces the need for as many experimental participants because they participate in both conditions of the study, (b) it is a powerful design because participants serve as their own controls, and (c) it is often the case that researchers want to measure participants more than once (e.g., across time) in an experiment. At the same time, however, repeated measures design has the drawback of not being applicable to all research situations. For example, if participants learn something critical to the research during a first measurement (e.g., how to solve a puzzle), then participation in the second phase would not be appropriate (e.g., if it involved solving the same puzzle). In the hypothetical sleep experiment, to use repeated measures, you would have to have a test that you could use more than once or two versions of the test that are comparable.

The fourth edition of the Publication Manual of the American Psychological Association (APA; 1994) was the first to recommend that human subjects in an experiment be called “participants” instead, as a more humanizing referent. This practice is followed in this research-paper.

Naturally occurring pairs refers to pairs of research participants who have some natural relationship (often biological in nature). It is much like matching, except that matched pairs are artificially paired, in contrast to these natural pairs. Examples of common natural pairs that researchers might use include twins, siblings, or littermates (for animal studies). For example, in an attempt to determine the effects of heredity and environment on IQ, researchers often work with identical twins separated at birth. Such twins have identical genetics, thus holding heredity constant between them. The twins might, however, differ considerably in their childhood environments—if one twin was reared in a high-quality environment (e.g., attentive parents, good schools, high socioeconomic class) and the other twin grew up in a disadvantaged environment, then we have a naturalistic study that is as close as we can get to an experiment comparing the effects of good and bad environments on IQ. Sometimes the relationship between naturally occurring pairs is not biological in nature; for example, a researcher might use husbands and wives as pairs because of the assumption that marriage would bring about similarities in the couple. The limit to using natural pairs should be fairly obvious: Many times an experimenter wishes to use participants who do not have any natural relationship such as those described; in this case, the experimenter can “create” pairs through the use of matching (described in 1).

Statistical Analysis

Lest you get lost in this forest of experimental design factors so that you cannot see the trees, let me remind you that this discussion has centered only on designs that have one IV and two levels. The reason that all of these factors have fallen under the same main heading is that all such designs require similar statistical analyses. Assuming that your DV yields interval or ratio measurement (see Chapter 6), any one-IV, two-group experimental design will use a t test for statistical analysis. The t test compares the size of the difference between DV means (in our hypothetical example, exam scores) of the two groups to the underlying variability. If the difference between means is large compared to the variability, then the researcher concludes that the difference is significant (probably not due to chance) and attributes that significance to the IV (see Chapter 6). This conclusion is possible because of the control afforded the experimenter by the experimental design.

The only difference in statistical treatment for the two-group designs depends on the assignment of participants to groups: You would use an independent-groups t test to analyze the results from this type of design when you have used random groups. On the other hand, if you used nonrandom groups, the proper statistical analysis would be a correlated-groups t test (also known as a t test for matched groups or dependent t test). This relation between experimental design and statistics is a crucial one—all designs lead logically and invariably to a particular statistical test. This reason is why it is critical for researchers to use a specific design when they develop their experimental ideas.

One-IV/Multiple-Groups Experimental Design

Discussing experimental design is a simpler matter from this point forward—not because the designs them-selves are simpler, but because you are now familiar with the important components of experimental designs and their vocabulary. For example, you should be able to read the description of this new design and immediately understand how it differs from the previous design (one IV, two groups). There is still only one IV, but there are now multiple groups based on that IV. If we go back to our hypothetical experiment looking at the effects of sleep, we would have to go beyond having only two groups for adequate and less-than-adequate sleep (see Figure 9.2). As you can see, in this hypothetical example, the researcher has added a group with even less sleep per night to the experiment. This group would sleep far less than is typical for most people and would provide a good contrast for a group that sleeps more than average (eight hours) and a group that sleeps about as much as average college students (six hours). Although Figure 9.2 shows three groups (three levels of the IV), there is no limit to how many levels of the IV you could have in your experiment. Reality, of course, probably does place a limit on how many groups you could have. Realistically, at this point, it may not make sense to add another group to this hypothetical experiment—we have an above-average sleep group, an average sleep group, and a below-average sleep group. Rather than adding more groups to this design, the researcher might conduct this experiment with the three groups and then determine whether further research with more varied sleep groups would be warranted.

Assigning Participants to Groups

All the other concepts that you learned about with regard to the simplest experimental design apply to the multiple-group design also. Chief among those other concepts is the assignment (or classification) of participants to groups. It is still possible to use random groups, typically by assigning each participant to one of the three (or more) groups in some random fashion. In this case, you would end up with three random groups so that participants in Group 1 had no relationship to those in Group 2 or Group 3, and so on.

Figure 9.2 Experimental design with one independent variable and three groups.

By the same token, you could also use one of the non-random strategies for assigning participants to groups. Because there are now at least three groups, the nonrandom strategies become somewhat more complex. For example, instead of matched pairs, you must use matched groups. Instead of simply matching two experimental participants on some variable, you must now match as many participants as you have groups. In our hypothetical example in Figure 9.2, we would need to match three participants in terms of age (or some other relevant variable) and then randomly assign each of them to one of the three sleep groups. If you use repeated measures in your experiment, you would need to have participants serve under all conditions in the experiment. Thus, participants would have to participate in more experimental conditions and for a longer period of time. Finally, using natural pairs would have to become natural groups. It is likely that this nonrandom strategy becomes least likely as you increase the number of groups. Instead of being able to use twins in your study, you would need triplets, quadruplets, or even quintuplets as your design got larger. Obviously, finding such participants would become exceedingly difficult. To use siblings, you would have to find larger and larger families; also, you could no longer use husbands and wives. The one situation that would still be likely for natural groups is animal littermates, assuming the animal species in question has large litters.

Statistical Analysis

Because t tests are appropriate for only two groups, a different test is necessary for the multiple-group designs (again, assuming that your DV yielded interval or ratio measurements). In these cases, you would use a one-way analysis of variance (ANOVA) to analyze your data, regardless of the number of groups in your experimental design. The term “one-way” simply refers to the fact that you have only one IV in the design—if you look at Figure 2, you can think of analyzing the data in only one way or one direction: across the design (comparing the three groups to one another). Analysis of variance refers to how the statistical analysis “works.” ANOVA compares the variability among the groups (the levels of the IV) to the variability within the groups (individual differences and error). If the variability due to the IV is large relative to the within-groups variability, then the researcher concludes that the IV has had a significant effect (see Chapter 6). This conclusion tells you that there is a difference somewhere among the means—unlike the t test, there are more than two means to compare, so it is not immediately obvious which mean(s) is (are) higher than the other(s). Additional statistical tests would be necessary to determine which groups (levels of the IV) are different from one another.

Two (or More) IV Experimental Designs

Based on Table 9.1, you might think that we have covered the majority of possible experimental designs—only about a quarter of the table is left to cover. However, experimental designs with two or more IVs are so numerous and used so often by experimenters that they are almost the standard type of design used in research. You will also notice from Table 1 that the decision-making process about choosing the appropriate design is simpler for experimental designs with more than one IV—you do not have to ask the question about how many groups or levels each IV has. Any design with multiple IVs falls under the heading of factorial designs because IVs are also known as factors; thus, as soon as you plan an experiment with two or more IVs, you know you will be using a factorial design.

Rationale of Factorial Designs

Researchers conduct experiments with multiple IVs because such designs allow a more real-world view of factors that affect behavior (DV). In a single-IV design, you are able to study only one IV’s effect on behavior at a time. In the real world, it is not very likely that our behaviors are affected by only one IV. For example, think about your score on the last exam that you took. If you stayed up all night cramming and took the exam with no sleep, you can certainly see how lack of sleep might have affected your score on the exam. However, was that the only factor that had an effect on your exam score? Of course not! What about your level of interest in the class, your physical health status, the number of other exams you had scheduled that day, whether you had a recent fight with your significant other, and so on? All of these factors (and many more) could have played a role in how well you performed on the exam. A factorial design allows you to study two (or more) of these factors as IVs simultaneously—it is somewhat similar to conducting two single-IV experiments at the same time.

Benefits of Factorial Experiments

The logic behind a factorial experiment is quite similar to that of a single-IV experiment—with one important change. In a factorial experiment, you want to determine the effects of two (or more) IVs on the same behavior or outcome. You could, of course, accomplish this same objective by conducting two separate single-IV experiments. There are two distinct advantages, however, to conducting a factorial experiment rather than separate single-IV experiments. First, you will typically save time by conducting only one experiment rather than multiple experiments. Second, the major advantage of a factorial experiment is that you get more information than you would from separate single-IV experiments. In both approaches, you would find out how each IV affects the DV—what is known as a main effect. In a factorial design, you will also find out how both IVs simultaneously affect the DV—which is known as the interaction of the IVs. An interaction lets you know whether the effect of one of the IVs on the DV depends on the particular levels of the other IV. Again, the possibility of an interaction provides a more real-world view of the behavior in question because most of our behaviors have multiple influences. An example should help clarify the concept of an interaction—a concept that many students find confusing at first.

Beals, Arruda, and Peluso (2002) conducted an experiment dealing with performance on an English proficiency test (the DV). (An aside: Beals and Peluso were undergraduate students at Mercer University when they developed and conducted this experiment; Arruda was a faculty member there.) They hypothesized that the format of the test (multiple choice or short answer—IV1) might affect performance on the test, particularly when taking into account the English proficiency level of the participants (proficient vs. limited proficiency—IV2). Indeed, their results showed a significant interaction (see Figure 9.3) between test format and proficiency level. Graphing an interaction often helps to make sense of the findings. As you can see in Figure 9.3, the two lines are not paral-lel—this type of picture is often a hint that the interaction of the two IVs is significant. Participants who were proficient in English made similar scores on the test, regardless of whether the test was multiple choice or short answer. Participants with limited English proficiency, however, scored much higher on the multiple-choice test than on the short answer test. From this example, you can tell that the effects of test format depended on the participants’ proficiency level. Or, you could say that the effects of the participants’ proficiency level depended on the type of test format. Either way that you describe the data, you can see that you must refer to both IVs simultaneously to explain the results of the significant interaction.

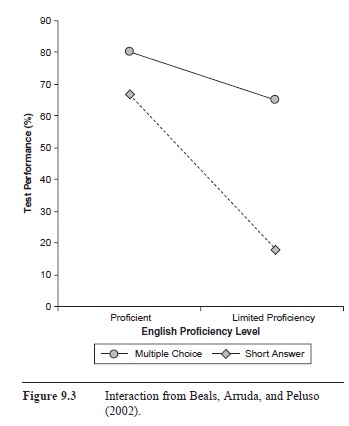Figure 9.3 Interaction from Beals, Arruda, and Peluso (2002).

Whenever you find a significant interaction, you should interpret it and not the main effects (the individual IVs) because the interaction renders the main effects meaningless. If the effect of one IV depends on the level of the other IV, then it makes no sense to refer to an IV on its own because, even if it showed a significant effect, the effect would not be straightforward. For example, in the Beals et al. (2002) study, it would not make sense to conclude that the multiple-choice test was easier—only the participants who were less proficient in English scored higher on the test.

Designing Factorial Experiments

Designing factorial experiments is a little like designing two single-IV studies and then combining them into one experiment. The simplest possible factorial design consists of two IVs, each with two levels. The standard way of referring to such a design is a 2 x 2 factorial design—the number of digits tells you the number of IVs, and the value of each digit tells you how many levels each IV has. Thus, if you had an experiment with two IVs, one with two levels and one with four levels, it would be a 2x 4 factorial design.

Returning to the hypothetical sleep experiment, suppose you want to add a second IV because you know it is common for people to drink coffee to “get going” in the morning; this behavior might be even more likely if a person got less-than-adequate sleep. Thus, you might want to determine the joint effect of amount of sleep and amount of caffeine—if less-than-adequate sleep does hamper test performance, might the effect of caffeine counteract that effect? There are almost limitless possibilities for designing this experiment, primarily depending on how many groups and what levels of the IVs you want to use. To keep things relatively simple, suppose that you decide to use only two levels of caffeine for the second IV, which you add to the last version of the sleep experiment (see Figure 9.2). You decide to administer the amount of caffeine (approximately) in two cups of coffee and to compare that to no caffeine. When you combine the two IVs, you end up with the experimental design shown in Figure 4—thus, you have a 2 x 3 factorial design.

Assigning Participants to Groups

As with the multiple-group design, you have to determine how to assign your participants to groups. You can use random groups or one of the nonrandom strategies discussed earlier. However, because you have multiple IVs, a new possibility arises: You could use random groups for one IV and nonrandom groups for another IV. This possibility is the reason that there are three possible experimental designs listed in Figure 9.1 for a factorial experiment. You could use random groups for both IVs, typically by assigning each participant to one of the groups of combined IVs in some random fashion. In this case, you would end up with random groups throughout the experiment so that participants in any given group had no relationship to those in any other group.

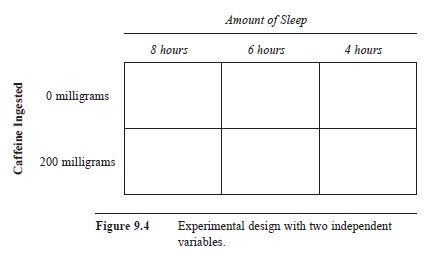Figure 9.4 Experimental design with two independent variables.

By the same token, you could also use one of the non-random strategies for assigning participants to all combined IV groups. Because any factorial design has at least four groups for two IVs, the nonrandom strategies become somewhat more complex. For example, you would have to have participants in all groups matched—or, for repeated measures, participants would have to participate in every possible condition in the entire experiment. Using natural groups becomes highly unlikely in a factorial design.

The third possibility, mixed groups, entails one IV with random groups and one IV with nonrandom groups. This option is a popular one, as researchers often like to measure random groups (IV1) over time (repeated measures—IV2).

Statistical Analysis

Just as with the multiple-group designs, you will use ANOVA to analyze the results from factorial designs (assuming, of course, that your DV yielded interval or ratio measurements). However, for such designs you would use a factorial ANOVA to analyze your data, regardless of the number of IVs in your experimental design. You might hear the term “two-way ANOVA,” which refers to the fact that you have two IVs (often referred to as A and B) in the design (or “three-way” for three IVs: A, B, and C) . In such a case, ANOVA still compares variability due to IVs to the variability within groups (still individual differences and error). In a two-way factorial ANOVA, however, you get results for each IV plus the interaction of the two IVs (A, B, and AB). As you add more IVs, not only do you get results for more main effects, but the number of interactions also increases rapidly. For three IVs, you would get results for A, B, C, AB (two-way interaction between Factors A and B), AC, BC, and ABC (three-way interaction among all IVs). With four IVs, you would find results for A, B, C, D, AB, AC, AD, BC, BD, CD, ABC, ABD, ACD, BCD, and ABCD (four-way interaction). As you might guess, it is rare that researchers use designs larger than three or four IVs.

Variations On Experimental Designs

Researchers often want to compare participants of different ages to get a glimpse at how behavior may vary or change over the lifespan. There are two approaches to measuring these differences—each is associated with a particular type of experimental design.

A powerful method for looking at changes during the lifespan is longitudinal research. In this approach, a researcher studies a group of participants over an extended period of time, measuring them repeatedly throughout that time. One of the best-known longitudinal studies is that of Lewis Terman, who began studying more than 1,500 gifted children (IQs above 140) in the 1920s. Although Terman died in the late 1950s, the study has continued and will not end until all of the original participants have died (http:// www.hoagiesgifted.org/eric/faq/gt-long.html). Because the researcher measures the same participants repeatedly, a longitudinal study employs nonrandom groups (repeated measures). Thus, a researcher conducting a longitudinal study would use one of the correlated groups designs in Figure 9.1.

As you can imagine, there are many barriers to conducting a longitudinal study. Two major problems are the long time involved in such a study and the difficulty in tracking participants over many years. To alleviate these problems, researchers developed cross-sectional studies. In a cross-sectional study, a researcher measures participants from different age groups at about the same, limited time. For example, you may have heard of the Nielsen TV ratings—they measure TV viewing habits of different age groups at the same time to determine how viewing habits vary by age. Although the basic purpose is the same as in longitudinal research, cross-sectional studies enable researchers to gather the data in a much shorter time period and to avoid the problem of tracking participants over time. Because the researcher measures different, unrelated groups of participants, cross-sectional research typically uses random groups and one of the random groups designs from Figure 9.1. If, however, a researcher wanted to ensure the equality of the groups before measuring them, matching might be possible. For example, if you are collecting TV ratings for different age groups but you worry that socioeconomic status might play a role in TV viewing habits, then you might want to use different age groups who are matched on socioeconomic status. In this case, you would use a correlated groups design from Figure 9.1.

Summary

Knowing the basics of experimental design is crucial to planning an experiment. If you simply “threw an experiment together” that did not fit a known experimental design, then you would have no way of analyzing the data and drawing conclusions from your research. Experimental designs give researchers a way of asking and answering questions about their area of interest—human and animal behavior, for psychologists.

References:

Beals, J., Arruda, J. E., & Peluso, J. P. (2002). The effects of language proficiency on test performance. Psi Chi Journal of Undergraduate Research, 7, 155-161.