This sample Cryptology and Security Research Paper is published for educational and informational purposes only. If you need help writing your assignment, please use our research paper writing service and buy a paper on any topic at affordable price. Also check our tips on how to write a research paper, see the lists of criminal justice research paper topics, and browse research paper examples.
Commerce in the modern world is based on virtually instantaneous electronic transmission of financial data including movement of money. The Internet has allowed us to move away from physical transactions via checks and currency. However, it is dependent on an unprecedented level of trust with an equally unprecedented potential of catastrophic financial loss. Illegal movement of money in the electronic form requires no physical access nor leaves physical evidence and can be accomplished from the other side of the world. Thus, the need for unquestionable security has arguably equaled or eclipsed that of military needs from just a few decades ago. With so much to gain and so little to lose, the criminal element has been transitioning to take advantage of every opportunity afforded by less than adequate security measures.
Security must be well planned, implemented, monitored, enforced, and reviewed. Use of encryption and decryption is an absolute necessity and thus must be more dependable than any time in the history of the planet. The cryptographic algorithms used ideally must not simply be rock-solid, but beyond question, thus our dilemma. At best we know that cryptography is a work in progress and we unfortunately cannot prove it is perfect, – we can only prove it is imperfect. We use computer systems and all the rest of the infrastructure knowing that it is flawed by virtue of being made by humans.
This short introduction notes some of the early methods which often translate into present-day concepts and vulnerabilities. Use of letter substitutions and transpositions defines early cryptology but was nevertheless a dependable method when used correctly. It has always been the misapplication of techniques that rendered cryptographic systems vulnerable. Topics include stream and block ciphers, passwords, and symmetric versus Asymmetric cryptography.
Fundamentals And Future Directions
One of the more dependable themes in modern entertainment is the thriller in which the supposedly impossible was done. Security of a bank, museum, or fortified building is breached, and something is taken defying incredible odds. Invariably many types of security systems are circumvented, and by luck, guile, and intelligence, the deed is done. Its comparable to an airplane crash in that not one, two, or even three things went wrong but a combination and other factors that caused the accident, any of which if recognized would have changed the outcome. Computer security can be viewed in much the same way. Human intelligence is a marvelous thing, but considering every possibility requires that people are perfect and humans can at best overcompensate for their inadequacy. Recognizing that advances in technology may swiftly undermine security, overcompensation should not be considered a luxury.
This short survey of cryptology begins with the above statement because it reflects reality. Every week it seems that another incredible security weakness has been exploited, usually resulting in or expecting to cause significant financial loss. Computer magazine, the flagship publication of the IEEE (the Institute of Electrical and Electronic Engineers) Computer Society noted in its October 2011 issue that “Hackers steal $13 million in 1 day via online security breach (Garber).” History has shown that criminals constantly get better; they find and attack the weak parts of physical and computer/networked systems where they exist and circumvent systems when they do not. Contributing on the positive side are white-hat computer hackers that test and evaluate systems, often discovering weaknesses and security holes that plague software written with too little attention paid to security.
The following document addresses the topic believing it to be fundamentally sound and capable of providing the security needed. However, like everything else in life, it is invariably the implementation and correct use of the system that complete the process. A simple password renders the best encryption system useless, and readers should understand any limitations will be exploited. At best cryptography and related security is a work in progress.
In the modern world, encryption and decryption via use of credit cards, security cards, passwords, and other tokens are part of everyday life and becoming ever more important. No one would ever think to leave a $100 note bill in clear view in their automobile or on their desk at work, but somehow they are not as concerned about a password which may represent significantly more financial risk. This disconnect with reality is the target of social engineering, attempting to obtain such information via sociological means. Although social engineering is not the specific topic of this document, it should be considered at each point of a security audit.
There are many approaches to address the topic of cryptology. A mathematical explanation is appropriate for those with the required mathematical background; however, this document will minimize formulaic expressions. Mathematics will be limited to numbers of possibilities and understanding the significance of large numbers (for a mathematical view, see Menezes et al. (1996)).
Several years ago a story was circulated around the Internet that began: “Aoccdrnig to a rscheearch at Cmabrigde Uinervtisy, it deosn’t mttaer in waht oredr the ltteers in a wrod are, the olny iprmoetnt tihng is taht the frist and lsat ltteer be at the rghit pclae.” While the attribution was wrong, the scrambled message makes a very important point. Breaking an encrypted message does not necessarily require getting every “t” crossed and “i” dotted. As a consequence, linguists and puzzle solvers were critically important in this field, and it is only the recent development of the computer-based cryptology that has reduced their need.
Keeping messages private has always been an obvious requirement for military or diplomatic endeavors. The general study of such matters is called cryptology. It can be divided into two disciplines: obscuring or inhibiting messages from being understood by some manner of encryption, the study of which is called cryptography, and the breaking of those coded messages called cryptanalysis. In general use, cryptology is often referred to as cryptography which may lead to some confusion. This may be further complicated by steganography, the concept of hiding a message in some fashion and which itself may be encrypted.
Often, the modern study of cryptology gives less recognition to early methods and origins, progressing quickly to complex computational methods which when used correctly can surpass the capability of being broken by even the most sophisticated computing system. While a general understanding of computer-based models is appropriate, its utility is beyond many criminals although those with a technical understanding or ability to employ those technically savvy should recognize that in fact it can be unbreakable. This document will therefore note various aspects of the historical development because the many possibilities remain useful in everyday life (Callery 2008). The classic document of cryptology leading into the computer age is The Code-Breakers (Kahn 1967) although some may find The Code Book a smaller and more digestible volume (Singh 2000). A shorter review can be found in the journal Cryptologia (Al-Kadi 1992.)
Perhaps the earliest and most obvious method of obscuring information was the written form when few people could read. Related to that was use of a different language. The royal courts in Europe invariably spoke a different language than the common mostly illiterate person of a given country, thus protecting conversations from workers and limiting interaction to all but the educated. Changing languages throughout the conversation or in written messages was almost guaranteed to protect information when the unintentional listener/reader is only marginally literate. We continue to employ this technique today to keep information about birthday parties or similar concerns from our children. This may also be accomplished by using more complex wording without necessarily needing to change languages, but children (and criminals) learn quickly.
During World War Two, the United States used the Native American dialect of the Navaho to communicate securely between marines. This technique could only work if the opposing side had no expertise in the language chosen which had been carefully predetermined. Navaho was selected from among a wide variety of American languages because the population of speakers was high enough to meet military needs in terms of number of recruits. Traditional Navaho words also had to be reinterpreted to describe modern military hardware and other issues which were not part of the language. In a similar way, the “language of the street” incorporates words that replace others such as drug names or various criminal acts.
Another simple method of passing such messages is to physically hide it such that the other side cannot find it. In early Roman times, a slave could have his hair cut, have a message tattooed on his head, and after hair regrowth, the message was hidden. Recutting the hair revealed the message after traveling to an appropriate location. Clearly not a mechanism for timely disseminating of information, it can have the advantage of hiding the message from the slave. Unfortunately for him, he need not be alive to convey the message.
Using a locked strong box was a viable option for sending messages and other more tangible items, but rather than a single lock, a system was devised to use two locks. The owner placed items needing protection in the box and secured it with their lock. It was sent to another person, and instead of opening the box, something he or she could not do without the appropriate key, they added their own lock via a second hasp and sent it back unopened to the sender. Upon the return of the box, the original lock was removed and resent to the previous sender. It could then be opened because only the original receiver’s lock remained on the box. However, this technique could be exploited by what is known as a “man in the middle attack.” This required the box be diverted to another person before reaching its original target, a second lock was added by the interloper, and it was returned to the original sender. If the owner had no verification that the box reached its original destination, its contents could be obtained by that intervening person, and the sender might never know what happened. This was a concern hundreds of years ago and remains an issue today with regard to digital information.
There are numerous other ways to physically hide information. A message can be scratched into a material such as wood then covered with a layer of wax to hide it. A heat source will reveal the message after the wax drips away. In early roman times, the use of pigmented beeswax was an artistic technique now known as encaustic; thus, a message could masquerade as an artistic work. A slight twist to the above process would include the use of invisible ink. Typically, this has involved the use of “ink” which is clear when initially used. The ink may be as simple such as lemon juice or a specific chemical compound or mixture. Revealing the message involves treatment of heat or exposure to a chemical spray. Today, we can add notes to computer documents, and they remain hidden in plain sight because most people do not know about or consider their existence.
Although the above methods work, eventually a need developed for a more capable system to convey complicated or lengthy information in a routine fashion. Usually, individuals encrypt and decrypt information themselves which implies another security concern – more than one party will know the mechanism. The ultimate goal of a cryptography system is to protect information even if adversaries understand how it works.
A fundamental concept was the substitution cipher where letters are substituted to obscure the message. The Atbash cipher used in the bible was perhaps not strictly for security purposes. Its name comes from its use, substituting the last for the first letter, the second from the last for the second letter, continuing as defined by the Hebrew alphabet. Another simpler cipher is ROT13 which rotates back on M the thirteenth letter. If you cut the alphabet in half between M and N and then slide the second half under the first half were A aligns with N, B with O, etc., you have a cipher that is easier to use. The message “hello” becomes URYYB and there is no confusion to complicate decryption. Letters can be transposed rather than substituted within words somewhat as noted above referencing Cambridge, but the anagrams generated are perhaps even less secure.
Another transposition example will show the concept with a very short message. For the message ABCDEFGHI, the first nine letters of the alphabet, simply write the first three on the first line, the second three on the second line, and the remaining three on the third. Reading down the first column and then the second and finally the third, we get ADGBEHCFI for the encrypted message. The mechanism or cipher needs to allow for uneven rows and is not limited to only three lines. Obviously, there are many other possible ways of manipulating the message, reading down one column and then up the following column or going backwards. The one limitation is that all letters in the original message are present and there are a limited number of words and messages that can be made from them. It is easy to understand that compared to transposition, substituting letters can make the encrypted message much more difficult to decrypt. However, adding simple transposition to other building blocks of encryption can dramatically increase complexity to the process.
An early device allowed for the simple sliding of one alphabet against another. This became known as the Caesar cipher because Julius Caesar used it with his generals. It consisted of two disks, one smaller rotating on the top of the other and both having the alphabet imprinted there on. This simple substitution is known as a cipher which is a series of steps followed to encrypt or decrypt a message. The original information is known as plaintext (often shown in lowercase letters) with the enciphered version (shown in small uppercase letters) known as the cipher-text. We can envision they can be lined up so that in English, the “a” on the top disk is aligned with the “a” on the bottom disk. Turning the smaller disk two letters to the left (Caesar used three letters), we can then use this cipher disk to encrypt a message. This movement of letters by two is the auxiliary information usually called the key or sometimes the crypto-variable (shown in uppercase letters). This is easier than Atbash or similar techniques because the letters remain in alphabetic order.
Using this substitution cipher above, the word “ate” becomes “CVG” and the line of text “encrypting data is one way to keep it secure” becomes “GPETARVKPI FCVC KU QPG YCA VQ MGGR KV UGEWTG,” which initially seems imposing (Table 1). This would likely be unreadable to someone with no cryptography skills but is nevertheless very weak. Removing the spaces will make the message look even more difficult but is no match for the cryptanalysis methods below. Difficulty of code breaking may also appear to be increased by using alien or nontraditional characters such as those taken from other languages, cultures, or additional fonts. This is deceptive only for those not familiar with encryption.

Each language has their own peculiarities, there are a limited number of letters which are repeated, and some letters occur in one order but never reversed. In English a double “h” is unlikely compared to a double “e,” and a “u” will follow a “q” but never in the reverse order. More important in deciphering messages are the frequency of the letters which cannot be hidden in the above examples. The standard frequency distribution of letters is different for a given language. Generally, in English the letter frequency order is E, T, A, O, I, N, S, H, R, D, L, C, U, M, W, F, G, Y, P, B, V, K, J, X, Q, and Z. A message of sufficient length or multiple simple substitution messages combined allow you to break the message. Simply replace the most frequent letter with E and the second most frequent with T and continue with all letters, and even if not perfect, the result is probably decipherable.
Another way of representing letters is to use not one but two or three characters. The benefit of this technique is a single letter can be represented by multiple combinations. When each letter is represented by two alphabetic characters, the number of possibilities is 262 or 676, thus providing 26 combinations for each letter if distributed evenly. Using three characters, the number is 263 or 17,576 with even greater possibilities. Thus, the letter “a” might be “AEL,” “MLT,” and “ZYE,” for example.
When two or three characters are used to represent one letter, not only can each letter have multiple representations but they might also key for words. Thus, “AML” might be code for “bank,” and “LTL” could translate to “dollars.” To decrypt a mixture of substituted letters and code words requires its’ nomenclator. Certainly one of the most historically important encrypted messages was known as the Zimmermann telegram and used a numeral-only nomenclator with numbers up to 99,999. The purpose of that telegram was to entice Mexico into World War One on the German side and keep the USA out of Europe long enough to subdue England. Having used the same nomenclator previously, it had already been partially broken, and its decryption was a significant point in the war.
The usefulness of this possibly more secure technique using a nomenclator is sometimes diminished by the necessity of agreeing on all likely code words beforehand and requiring a code book. If security is the purpose, the nomenclator must be stored and used securely to not fall into the wrong hands. But as noted above, increasing use results in decreasing security.
To expand the possibilities of the Caesar cipher and increase its complexity and thus security simply requires not keeping the disk or substitution the same. If, for example, the first letter is moved by two and the second by four, “ee” now becomes “GI,” and if repeated, the result is not so obvious. That initially makes the cryptanalysis more difficult, but using frequency analysis it would eventually be recognized that there are two different groups of letters – the simplest polyalphabetic cipher. The natural end to this technique is to use all the possibilities and was ultimately done by Blaise de Vigene`re (see Table 2). Continuing on the same road, what if a word was used for the cipher key? If the word “CIPHER” was the cipher, that would mean lining up the “a” with the “c” and using the wheel to determine the first letter and then lining up the “a” with the “i” for the second letter. After the sixth letter a lined up with “r,” the same code is repeated until the message is complete. As the code word cipher becomes longer, cryptanalysis becomes ever more difficult but not impossible.
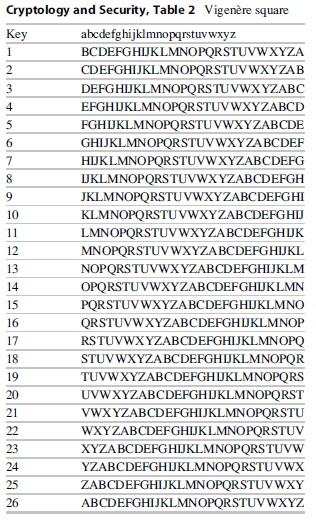
Up to this point in the development of cryptology, the cryptanalysts were winning but that was about to change. Consider what happens if the code keyword is 100 random letters from a to z, now the encrypted message becomes extremely difficult to break. True randomization makes the encrypted message random characters and thus unbreakable when used correctly. One important requirement becomes access to truly random numbers. Before computers became available, the process of generating random numbers might be similar to the numbered balls used for lottery drawings. However, because encryption has become ubiquitous and the need for random numbers dramatically increased, we are limited to computer-generated or pseudorandom numbers. Such numbers may not be perfectly random but are sufficiently random to not reduce the security of the encryption. For cryptographic purposes, the process of random number generation must be verified to ensure quality, or unbiased random numbers are generated.
During World War Two, making a cipher unbreakable involved using a one-time pad, a piece of paper with key codes. Critically important is that it is only used once. Codes repeatedly used create patterns cryptanalysts use to break the code. Judicious use of a sufficiently long and truly random one-time pad may fulfill the cryptographic needs, but it creates other problems – it is only as secure as the one-time pad, and transmission of such information creates its own problems. When the adversary finds 30 days or more of one-time pads, because they may already be disseminated to ships at sea, for example, you may have lost the ability to keep messages secret. Likewise, given the length of the one-time pad should be at least as long as the message itself, this unbreakable method is unfortunately of limited utility in the current world.
By the early 1900s, there had been sufficient interest in cryptography to entice inventors to attempt making devices to accomplish this task. The best documented is the Enigma machine used by the Germans in World War Two which was an electromechanical device to encrypt/ decrypt messages. It might be simply described as an electrical–mechanical version of multiple Caesar cipher disks called rotors, chained together such that when a typewriter key is pushed, the result is an illuminated letter. It had the possibility of being nearly unbreakable, but the allies had one so they knew how it worked and it was misused. The Germans essentially repeated a portion of the same message each day because the daily weather report began with the same words. Thus, if settings on the Enigma could be manipulated to decrypt the cipher-text back to those words, they could decrypt the entire message. Although this was not an easy task given the state of computing devices, it allowed messages to be broken with hard work. Not every transmitted message would be decrypted, and those that were might not have been decrypted in time to be useful.
The above examples are based on traditional characters or ones that replace those characters. With the advent of computers, all characters were replaced by a binary code, strings of ones and zeros. Seemingly elementary this enabled a vast and wide-ranging new world of unprecedented complexity. For the uninitiated, a simple example is no further than a typical garage door remote. To set or change the code, you open it and move the 8, 12, or more switches in both the sender and receiver. (Leaving the original settings unchanged is the same as keeping the default password on a computer – it is only marginally better than not having a password or code.) Eight similar switches grouped together are known as a computer byte.
A byte consists of 2×2×2×2×2×2×2×2 possibilities also represented as 28 or mathematically as 256 possibilities. This respectively represents a doubling of possibilities with each additional character or 2, 4, 8, 16, 32, 64, 128, and 256. This is a key concept because the code possibilities increase geometrically, while the ability to test a code or pass-phrase is linear (Table 3). This has a dramatic effect as passwords get longer, and the difficulty of breaking passwords becomes increasingly difficult depending on the current state of the art of cryptanalysis. If we spend twice as long inputting pass-phrases, we have only attempted twice as many codes. Ultimately, the trade-off is defined by the cost of breaking the code (the computational expense) vs. the worth of the protected information.
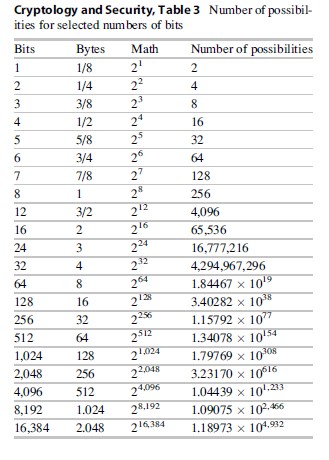
By choosing the option of 12 bits on a garage door opener, we effectively have a byte and a half or 2×2×2×2×2×2×2×2×2×2×2×2×2×2 possibilities also represented as 212 or 4,096 possibilities. This is not an overwhelming number, and a device that produces all possible signals simulating all garage door-opening possibilities is easy to envision. Another byte (220 or 1,048,574 possibilities) of additional complexity would make it increasingly unlikely that a code generator could produce all the possible code signals in a short span of time. The garage door opener is a security device meant to keep honest people honest and cannot be considered sufficient to protect someone that has been targeted by those with criminal intent.
Although computer technology may have been pressed into the cryptology arena very early because of world wars, passwords were not the initial concern. Nevertheless, we use them every day and they contain information which may be built upon to understand others’ aspects of cryptology. Portrayal of the mathematical complexity of password encryption is difficult and most obviously incorrect in popular media. Breaking a password is often presented as identifying each character, one at a time in sequence, which might accurately represent a safe cracker listening to the tumblers fall in place using stethoscope on an old-style safe but has nothing to do with passwords. This is particularly disconcerting because, as any computer or ATM (automated teller machine) user inherently understands, you either get the password right or you do not. Unfortunately, the underlying message conveyed to the public is that passwords cannot be safe and are easily broken, thus unintentionally undermining the need for using good passwords. Believing you know all but the first or last character of a password is the same as not knowing the password. At that point, it seems only a brute force attempt at breaking the password or portions believed to be unknown will allow it to be determined. A brute force attack means trying every possibility until the correct one is discovered. The goal of the cryptographer is to limit access to only the correct password or a brute force attempt because the latter is defined by the state of computing technology and the implementation of the system. But this only works dependably if the user has a good password, hereafter known as a pass-phrase, and keeps it protected.
Use of pass-phrase instead of password is an important change meant to entice and empower the user into choosing more secure passwords. The user need not have to remember a passphrase; it can be recorded on a piece of paper and subsequently stored in a wallet or purse.
Thus, it is considered as important as money, credit cards, and other information which the user intentionally keeps out of reach by others. Regardless of complexity, the user ultimately remembers the pass-phrase even if it takes several days. However, it should therefore be obvious that requiring frequent pass-phrase changes discourages use of strong pass-phrases and conveys the entirely wrong message.
With regard to pass-phrase parameters, two important factors are complexity, known as entropy, and length. Entropy is dependent on the possibilities of the pass-phrase. If a user is limited to only numbers or 0 to 9, the difficulty of breaking it is much reduced. Normally, systems should allow pass-phrases consisting of the alphabet containing 26 upper- and 26 lowercase letters along with the ten digits and a variety of special chapters. The standard for keyboard input is the ASCII (American Standard Code for Information Interchange) table and consists of 128 possibilities. Key combinations with the Ctrl, Alt, and other keys can dramatically increase the number of possibilities. But because every input device does not have every character or modifying keys, even the standard ASCII list of 128 may be impractical.
The much more important factor is passphrase length. If the pass-phrase is limited to 26 letters (case being irrelevant), ten numbers, and four special characters (e.g., @, #, $, and %), that would be 40 characters. Therefore, using only one character, the number of possibilities is 40, and with two characters (402), the number of possibilities increases to 1600. Moreover, using six characters (406) dramatically increases the possibilities to over four billion. (Note that using repeating characters such as 111111 for a pass-phrase is more likely to be observed, and thus, systems will generally limit the number of repeated characters to two.) Similarly, if upper- and lowercase letters can be used (52) and numbers (10) and eight special characters, one additional character increases the possibilities by a factor or 70 and even more substantially with additional characters.
Assume you have 70 possible characters and you are required to have an eight-character pass-phrase. That would be 708 or 576,480,100,000,000 possibilities. You could correctly guess the pass-phrase the first time or the last time, but on average it would require trying half of the possibilities or take 288,240,050,000,000 attempts – a brute force attack. If you try one every 10 s, it would take 48,040,008,333,333 min or 91,400,302 years to guess the pass-phrase on average for someone using a good pass-phrase. That seems like reasonable security risk but assumes the system will let you continuously attempt to input the pass-phrase without slowing down or stopping, an obvious implementation error. But more importantly, it is a good idea because we do not know how technology might change in the future.
Knowledge of a person can sometimes be used to guess a pass-phrase: the name of an owner’s dog or other known or easily obtainable information is a poor choice, and their use perpetually hounds the lives of celebrities. Generic bad pass-phrase lists can be found on the Internet and invariably include the word password. The next and most likely mechanism to correctly guess the pass-phrase is by what is known as a dictionary attack. They involve trying all words and probably some simple derivatives also including foreign language words. That files exist purposely for dictionary attacks should be considered from a positive point of view; they emphasize the need for a good passphrase. Although many types of specific cryptanalysis attacks exist, they are relegated to longer texts, and the only remaining possibility for a pass-phrase is a brute force attack. Guidelines for choosing pass-phrases exist, but only systems which require complexity (at least one letter, number, and special character), define minimum length, and limit character repetition can ensure sufficiently secure pass-phrases are used. Often they allow pass-phrases to be reused after some number of changes or allow changing to very similar pass-phrases, another potential risk.
Secure systems do not allow continually trying pass-phrases which is a necessity but also problematic in itself. If a system only allows three attempts before blocking an account, a given account can be rendered useless if anyone can try three one-character pass-phrases to block it. The price for this type system must include the cost of an administrator required to frequently reset pass-phrases and both time and effort diverted from the user’s efforts. Another method to deal with such problems requires the user to wait 5 min before he or she can again attempt to login, and only after a greater number of attempts is the account blocked requiring an administrator reset. Giving the user a method for self-resetting of pass-phrases is another option but is itself a security consideration.
The mechanism used by the system to process pass-phrases is often not known by users, they just assume it is recorded somewhere, and when the correct pass-phrase is input, the user gains the appropriate access. It should be obvious that if the user’s pass-phrase is compared to a recorded version, then the pass-phrase must be available in some way which is necessarily a security issue. Thus, for security reasons, such a process is no longer used, and in fact generally pass-phrases should not be known by anyone except the user.
Instead of keeping the pass-phrase on the computer to compare it with input, a hash of the passphrase is saved. As the word hash implies, the pass-phrase is essentially chopped like the meat and potatoes combination with the same name. A computer hashing algorithm (used interchangeably with cipher) converts the input to a string of characters that cannot be reconstituted. It is a secure one-way function.
The hashing process is similar to the CRC or cyclic redundancy check that quickly checks to determine if a file is believed to be the one associated with the file name. However, CRC is not intended to be a secure check as with the passphrase hashes noted above. Nevertheless, it is extremely difficult to create an illegitimate file with the same CRC value also having the same name as what it is attempting to impersonate. This is what makes the CRC value such a useful tool to monitor file changes.
For the hashing algorithm (examples include MD-5, Whirlpool, and CRC-16) to work as a test of pass-phrase accuracy, the same pass-phrase must always result in the same hash value. Fortunately, system administrators need not know a pass-phrase for a specific user; they merely need access to change a pass-phrase. Changing the pass-phrase to something different and subsequently requiring the user to change it again within a few uses helps to ensure the system limits what system administrators can do when all such activity is recorded or logged. However, hackers routinely erase or modify logs in an attempt to hide their tracks.
Several examples of text that has been hashed give the reader an appreciation for the technique shown in Table 4. The examples are derivatives of the text “Encrypting data is one way to keep it secure.” Each line is hashed using two algorithms. First is the shorter CRC-16 (cyclic redundancy check) of 16-bit or 2-byte length and designed for quickly checking to see if a file has changed. Converting the larger text to only four characters of the resulting hash shows the power of a simple hashing algorithm. (When the results do not include letters above F, it indicates that characters are hexadecimal or base 16 which includes numbers 0–9 and letters A, B, C, D, E, and F.) For this simple example above, I used the free program Easy Hash v. 1.6 by Tomasz Kapusta to generate the hashes, but similar programs can be found on the Internet. The more complex SHA-1 is a widely used hash algorithm and has a 20-byte or 160-bit length equivalent to 40 characters. It was designed for the US National Security Agency in 1995. Although each line in the example only differs from the first line by an extra space or the case of one letter, the result of the hash is dramatically different. SHA-1 received extensive testing before being selected by the NSA, but, like all widely used algorithms, eventually attacks will reveal weaknesses, and this will soon be replaced by a more secure standard.

Unfortunately, users can create situations that require a correct pass-phrase to be used without the ability to simply change it. An example of this issue is when a drive, folder, or file is securely encrypted and does not come under the control of an administrator and the person in question has lost/forgotten the pass-phrase or is no longer available. If the pass-phrase is cryptographically sound, then the protected entity essentially no longer exists because breaking that pass-phrase maybe virtually impossible. As encryption of data becomes more popular with individuals, important family information is put into jeopardy if that person has not given the pass-phrase or key to their lawyer or other family member.
A more secure way of protecting critically important information is to use a technique whereby multiple users are required to find the correct pass-phrase. This can be envisaged using an X, Y grid. Assume the correct pass-phrase is located at zero on the Y axis and is equivalent to some number X. For simplicity we will use the pass-phrase at 10, 0 (X, Y) on the grid. A straight line can be drawn through that point and through points 11, 1 and 8, -2. Knowing any two points anywhere along the line will define the line and thus define the pass-phrase as 10 because that is where the line passes through the Y axis. Ten different people could be given different X–Y coordinates, and any two can determine the pass-phrase, but one person alone could not define the Y axis location. In a similar fashion, use of other mathematical functions can require three or more sets of coordinates to define where the line crosses the Y axis. Thus, collusion or compromising one point does not immediately compromise the pass-phrase, but its complexity does not warrant use for anything except critical data. However, whoever controls the system is therefore another security consideration.
Given the limitation of some number of characters for a pass-phrase, it is possible to generate all the possibilities for a given hashing algorithm, saved as a “rainbow table.” These are available on the Internet but are large, in the range of a terabyte or more. Thus, if one can obtain the hashed pass-phrase, locating it in the table will produce the originating pass-phrase. This works because a comparison of results of hashing programs should generate the same hash although in use, and unbeknownst to users, the result can purposely be different. Just as adding salt to food hash will change it, adding a salt (an additional factor) to a hashing algorithm changes its result as well. For example, simply appending an additional single character to the end of each pass-phrase will change the hashed result dramatically, as implied above and thus rendering a hash table useless. Because the same character is added each time to each pass-phrase, the resulting hash will be the same for each specific passphrase but will be different from the non-salted pass-phrase.
Probably the most simplistic and yet elegant operation in computer-based cryptology is the Exclusive Or Logical Operator also known as XOR (pronounced X-Or). It is symmetrical, meaning it works the same for both encryption and decryption. Remembering that computers deal with 0 s and 1 s, it is obvious that they work well with logic table based on true and false (Table 5). Given the result, this is a deceptively simple operation. The message (line 1), a string of 0 s and 1 s, is XORed with the key (line 2) also a string of 0 and 1 s. The key and the encrypted message are lined up, and for each bit, if both are 0, or both are 1, the resulting encrypted bit (line 4) is 0. Conversely, if they are different, the unencrypted bit is a 1.
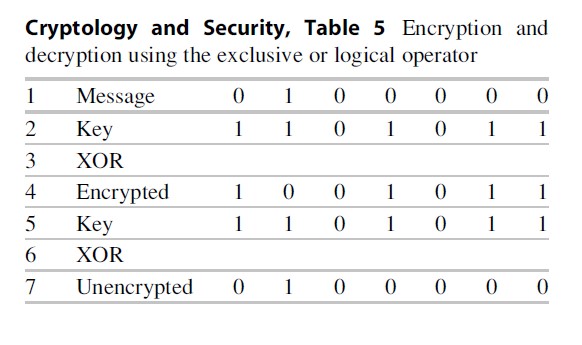
Un-encrypting the encrypted message works the same way. The result is the original message (line 7). This is a very fast operation with security dependent on the key. A short simple key of eight bits (256 possibilities) can be broken easily, while a non-repetitive random key is essentially the one-time pad and cannot be broken when used correctly. Therefore, we continually increase the key length for secure functions with 256 bits (1.15 1077 possibilities) on the horizon and even longer keys available as that eventuality is expected.
Most of the above consists of cryptographic basics and how they may be used. Many operations are chained together to increase the difficulty of cryptanalysis. Much of what is used consists of the two major types of modern ciphers which include stream and block types. The stream cipher may be considered similar to the XOR system above and the one-time pad. It encrypts and decrypts the message bit by bit but is very fast. Unlike the one-time pad which requires a key as long as the actual message, the stream cipher uses a key stream generated with a much smaller key. An example of a stream cipher is RC4.
In contrast to the stream cipher, the block cipher, as the name implies, processes the message blockwise or equally sized chunks. Over time the block size has been increasing to stay ahead of more capable cryptanalysis techniques and computer advances. The minimum length has moved to 128 bits but will continue to increase. Actual use may be similar to the polyalphabetic substitution noted above, but as expected it is not that simple.
Block ciphers might be compared to a chain knot in that each subsequent knot is dependent on what goes before it and is therefore unlike the stream cipher in that a single missed bit might not obfuscate the whole message. Security is enhanced by repeating the simple function known as a round. Multiple rounds and other manipulations the security. Recognizing the need for such a cipher for nonmilitary or official uses led the US government to release a standard, the Digital Encryption Standard in 1976. With only a 65-bit key length, it was considered obsolete no later than 1998 when it was broken, but a variant – Triple DES – was used in its place. A competition resulted in the Advanced Encryption Standard or AES being released in 2001 after several years of testing. Other well-known block ciphers include Blowfish, Serpent, and Twofish.
Both stream and block ciphers are symmetrical, meaning they are used for both encryption and decryption. Cryptography had only been symmetrical until the 1970s when asymmetrical ciphers were first created. Conceptually, this would be more secure because previously the key was the same in both directions, and therefore, more than one person would need to know the key.
One inherent security problem that existed was the inability to protect a symmetric key. This was finally solved using a key pair or what is known as public key cryptography (Diffie and Hellman 1976). Initially, its strength relied on the difficulty of factoring prime numbers of very large numbers and more recently elliptic curves. A key pair is generated with one used as a private key and the other a public key. The significance of the keys is simply that at least one is kept secret and which is irrelevant. The most important consideration is that a cryptographically secure key needs to be much larger than others mentioned above, 1,024 bits or 128 bytes (representing 21024 or 1.8 10308 possibilities) which makes it a noticeably slower, on the order of a thousand times slower. But the additional time and key length is used to encrypt a key which is subsequently used in the much faster stream cipher above to encrypt or decrypt the message.
Consider a simple scenario with email; someone sends you a message which is encrypted with your public encryption key which might be posted on the Internet for anyone to use. Note the similarities between this example and the locked box scenario above. You in turn decrypt it with your personal key. Because a different key is needed to decrypt the message, anyone could send a message to you, but only you, by virtue of the fact that you have the private key, can decrypt it. Although this sounds of little use by itself, consider that the original message is encrypted using the sender’s personal key and also encrypted using your public key. The result isa message that could only be sent by the originator because it is encrypted with their private key (you decrypt it with their public key) and subsequently only you can decrypt it with your private key because it was also encrypted with your public key. While governments and corporations may question its use, consider that the vast majority of email is unwanted spam and that public/private key encryption could dramatically reduce unwanted email. It could significantly impact both network bandwidth concerns and infrastructure costs but is unlikely to become a standard.
The above represents a very limited introduction to cryptology without considering possible future developments. A new technology like quantum computing having the ability to much more quickly break codes makes constant vigilance a necessity for cryptographic security professionals. Ramifications of these or other new technologies make cryptographic security always a work in progress. But no matter how much we focus on the technology, that cannot be the end or as Bruce Schneier (2004) put it “I’ve realized that the fundamental problems in security are no longer about the technology; they’re about how to use the technology.”
Bibliography:
- Al-Kadi IA (1992) The origins of cryptology. The Arab contributions. Cryptologia 16(2):97–126
- Callery S (2008) Codes and Ciphers: all the tips and tricks you need to make them and break them. Harper Collins Publishers, NY, NY.
- Diffie W, Hellman ME (1976) New directions in cryptography. IEEE Trans Inf Theory 22(6):644–654
- Garber L (2011,October) News briefs. Hackers steal $13 million in one day via online security breach. Computer p 15. IEEE Computer Society
- Kahn D (1996) The code-breakers: the comprehensive history of secret communications from ancient times to the internet. Revised edn. Scribner, NY, NY.
- Menezes A, von Oorschot P, Vanstone S (1996) Electronic format 1997 (www.cacr.math.uwaterloo.cc/hac). Handbook of applied cryptography. CRC Press
- Schneier B (1996) Applied cryptography: protocols, algorithms, and source code in C, 2nd edn. Wiley, New York
- Schneier B (2004) Secrets & lies: digital security in a networked world. Wiley, New York, p. 398
- Singh S (2000) The code book: the science of secrecy from ancient Egypt to quantum cryptography. Anchor Books, Random House
See also:
Free research papers are not written to satisfy your specific instructions. You can use our professional writing services to buy a custom research paper on any topic and get your high quality paper at affordable price.





