Economics of Aging Research Paper

This sample Economics of Aging Research Paper is published for educational and informational purposes only. Like other free research paper examples, it is not a custom research paper. If you need help writing your assignment, please use our custom writing services and buy a paper on any of the economics research paper topics.

Population aging is a worldwide phenomenon. The demographic transition from a state with high fertility and mortality rates to a state with low fertility, low mortality, and increased longevity has changed the well-known population pyramid into what looks more like a rectangle or a skyscraper. This means fewer children and more old-aged people in relation to those of working age. Aging started in the industrialized world and has thus gone farther in these countries than in developing countries, where it started later. The transition is far from complete in the industrialized world, and aging is forecast to go on during the entire period of prognosis, up to the year 2050.

Population aging has caused anxieties about the economic effects of aging: the possibilities of supporting an increasing number of older persons with a shrinking workforce. This research paper focuses on the economics of aging in the industrialized world. The next section describes the demographic changes and aging, their history and prognoses of future development. The following section uses a life cycle approach to give a theoretical foundation for analyzing the economic aspects of aging, from both the individual’s and society’s points of view. Later sections analyze the effect of aging on production and consumption patterns. As old age pensions constitute such a large part of life cycle redistribution, special attention is given to pensions and the eventual strain caused by aging. The conclusions from these sections are that demographic changes will cause substantial economic pressure, ceteris paribus. The final section discusses possible remedies and concludes the research paper.

Aging Populations

Historically, aging started with a drop in fertility rates, which had already started to decline in many industrialized countries in the nineteenth century. In 1950, the total fertility rate was 3.45 in the United States (meaning that on average each woman was expected to give birth to 3.45 children), 2.66 in Europe, and 2.75 in Japan; it had fallen to 2.04 in the United States, 1.41 in Germany, and 1.29 in Japan by 2000. A fertility rate below 2.1 is below reproduction rate; the population will eventually shrink if immigration does not compensate for the low fertility. There is a rather large dispersion in fertility rates between countries within Europe, with Italy and Germany having the very low fertility rates of 1.29 and 1.35, respectively, while Sweden has a fertility rate of 1.67 and the United Kingdom 1.70 (United Nations, 2007).

It takes some 20 years before a birth cohort enters the labor market. Thus, low fertility rates will give rise to successively smaller cohorts entering the labor force.

In the next phase, population aging was driven by a drop in mortality and increases in longevity. Between 1950 and 2000, life expectancy at birth increased by 8.5 years in the United States, 11.2 years in Germany, 13.9 years in Italy, and 18 years in Japan, and population prognoses forecast that life expectancy will increase by at least 5 years by 2050 (United Nations, 2007).

A way of measuring aging is by dependency ratios, where the child dependency ratio is the number of children in relation to the number of people of working age, and the old age dependency ratio is the number of people aged 65 or older in relation to those of working age. The development of these ratios is shown in Table 57.1.

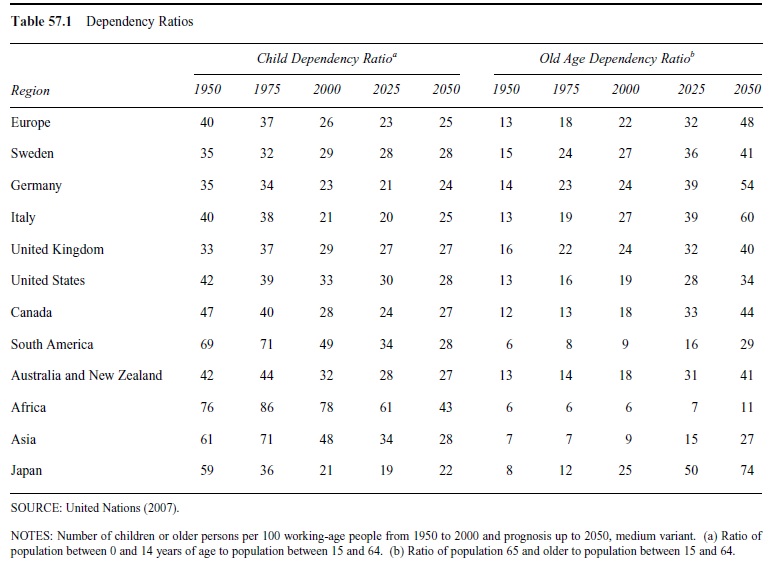Table 57.1 Dependency Ratios

As can be seen in the table, aging started in most regions and countries with a drop in fertility; the child dependency ratio fell. In the next phase, population aging gave rise to increases in the old age dependency ratio. The table shows that aging has been going on for a long time and is forecasted to continue.

Table 57.1 shows the UN population forecasts with the medium variant. It should be emphasized that demographic forecasts are highly uncertain. For example, fertility rates have shown great variability in the past; the forecasts assume a constant fertility rate. Also, so far, the drop in mortality has constantly been underestimated in population forecasts, as have the increases in longevity. Even with great uncertainties in the forecasts, there is no doubt that the population is rapidly aging.

Aging brings forward changes in consumption and production patterns.

Life Cycle Approach

No human being can support himself or herself by his or her own labor during a whole lifetime. Infancy is an obvious example, as is old age. Figure 57.1 sketches some important economic events in an individual’s life: entrance into and exit from the labor market plus the length of retirement period. Individuals need to consume in periods when they do not have any income. To survive, individuals have to cooperate. The main institutions for cooperation are the family, the market, and the state, which exist side by side, and their importance differs in different countries as well as historically in the same country. The way of mixing the institutions and organizing them has effects on the pressure caused by aging, as is evident later on in this research paper; for a comprehensive analysis, see Lars Soderstrom (2008).

E is the time of entry into adulthood and the labor market. Childhood extends up to the point E. The period from E to EX represents working years; EX is the exit from the labor market into retirement. D is the time of death; the period between EX and D is the number of years as a retiree. During the working years, the individual earns an income, assumed to increase with age. Assume that the individual wants to maximize lifetime utility, subject to the budget constraint determined by lifetime income. The planning problem is then to transfer income from working years to nonworking years and to smooth consumption possibilities.

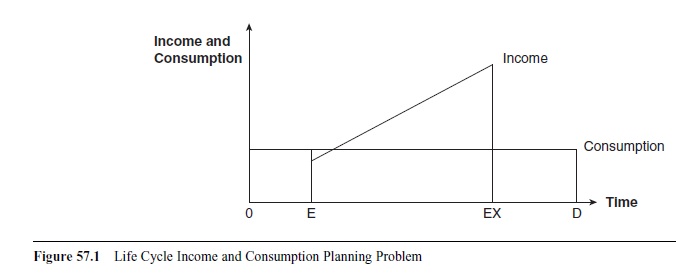Figure 57.1 Life Cycle Income and Consumption Planning Problem

The assumptions in Figure 57.1 are that income is increasing with age and that an even consumption stream over the years maximizes utility. Of course, other patterns are possible; they are discussed in the analysis of aging and the welfare state.

Figure 57.1 may also be used as an illustration of a society at a specific time. The number of children is then the number between origo and E, the number of people of working age is between E and EX, and the number of retirees is between EX and D. The income of those in working years is used for the support of all coliving individuals.

The figure highlights the planning problem faced by the individual and society—that is, how to organize transfers over years and between generations in an efficient and utility-maximizing way. The figure is drawn as if there were total certainty in life, the income stream is certain, the possibility of working until the age of EX is certain, and the time of death is certain, to mention but a few uncertainties that one meets in real life. Apart from childhood and old age, the risk of periods of work incapacity during working age, due to sickness or unemployment, for example, are examples of individuals’ inability to always support themselves. The purpose of the institution for cooperation—be it the family, the market, or the state—is then not only to even out consumption possibilities over the life cycle, but also to function as an insurer against income losses, the risk of high consumption needs, like health care and old age care, as well as poverty.

The life cycle illustration gives an intuitive insight into the problems that an aging population might cause. The following sections analyze it further.

Production and Labor Supply

So far we have shown a purely demographic view. However, more important from an economic point of view is the labor force in relation to the number of people being supported. At any given time, the number of people being supported is determined by the demarcation line between childhood and adulthood, between working ages and retirement, and finally between retirement and death. The UN figures used in Table 57.1 with the delimitation of age groups 0 to 14, 15 to 64, and 65 and older do not describe the economic-support reality in the industrialized world. In Western societies, there has been a trend of postponing entrance into the labor market. The expansion of higher education means that an increasing portion of each cohort studies at high school and university and delays entrance into the labor market. Besides, retirement age has shown a declining trend for several decades, even if it seems to have turned upward the in last decade. Economic growth is a common explanatory factor for both trends. Early retirement occurs both because pension systems have subsidized early retirement (see Gruber & Wise, 1999, for international comparisons) and because leisure is a normal good with positive income elasticity.

Furthermore, what is economically important is labor supply. Table 57.2 shows total labor force participation rates and the participation rates in different age groups.

Table 57.2 Labor Force Participation Rates in Different Age Groups, 2007

If the labor force is defined as people between 15 and 64 years of age, the participation rate is around three quarters in the countries shown in the table, far less in Italy, and somewhat higher in Sweden. Labor supply changes over the life cycle, with a rather low supply in young and old ages. The ages between 25 and 54 may be seen as the most productive years with high participation rates. The differences between age groups mean that the age structure and changes in it will influence a country’s production capacity.

Using labor force participation figures for calculating what might be called an effective old age dependency ratio gives quite different and higher ratios than the ones shown in Table 57.1; see Table 57.3.

The use of the labor force instead of the number of persons increases the old age dependency ratio by 6 percentage points (for the United States) at the least and 18 percentage points (for Italy) at most—that is, quite substantial increases. Moreover, the use of population figures to forecast the old age dependency ratio in 2050 gives substantial increases in the ratio, as seen in Table 57.1. The effective old age dependency ratio exceeds these significantly; by the middle of this century, there will be one retiree per working person in Japan and almost one retiree per working person in Italy. However, even these figures are underestimates if we are interested in actual work performed; unemployed people are included in the labor force, as are people on sick leave, holiday, and parental leave. In addition, participation rates only partly capture the labor supply; they do not tell how many hours per week or how many weeks per year a person works, or how many years constitute a working life. All these aspects matter, and the research paper comes back to this when discussing pension systems.

These future prospects have given rise to numerous alarm reports, but these are often built on static calculations. It is worth emphasizing that economies are flexible and that there are adaptation possibilities. Prices will change, giving incentives to adapt to new circumstances. As an example, there is empirical evidence from cross-section and time-series data that a slower growth in labor force induces a more rapid productivity growth (Cutler, Poterba, Sheiner, & Summers, 1990) Furthermore, institutions matter; the way of organizing life cycle redistribution and support of older persons will most certain change.

The last 50 to 60 years have seen important changes in the labor market and in different groups’ participation in the labor market. One trend is the increase in market work by women. There has also been a very marked downward trend in the participation rates by older men. Lately, this trend seems to be taking a turn upward. Gary Burtless (2008) shows that there is a trend of postponing retirement in industrialized countries; the age at retirement is increasing. Gabriella Sjogren Lindquist and Eskil Wadensjo (in press) discuss factors behind the decision to exit the labor market. They divide these into individual factors, such as health, family situation, and social and occupational pension schemes, influencing the supply side, and institutional factors, such as wage system and mandatory retirement age, influencing the demand for older workers. They conclude that the closing down of roads to early exit and the reformed pension system has delayed retirement in Sweden.

Table 57.3 Old Age Dependency Ratios, 2005 and 2050

Aging and Capital

Aging may also influence savings and capital accumulation. Albert Ando and Franco Modigliani’s (1963) hypothesis of consumption and saving over the life cycle assumes borrowing during childhood, positive saving during working ages, especially during the later phase of working ages, say between 50 years of age to 64, and dissaving during retirement. There is empirical evidence to support the theory—among others, Solveig Erlandsen and Ragnar Nymoen’s (2008) empirical study of private consumption and capital accumulation using Norwegian data strongly supports the theory—even if some contrasting evidence also exists.

The population forecasts show that the number of people in working ages will decrease, which means that capital per worker will increase, other things being equal. If the capital-labor ratio was optimal at the outset, there will be too much capital; savings can be reduced and consumption increased. This is a conclusion drawn by, for example, Cutler et al. (1990). However, with fewer workers to support an increasing number of older persons, an increase in productivity caused by more capital per worker should be a welcome effect. The effect of aging on savings and capital is further analyzed in the discussion of pension reforms.

Production and Consumption Patterns

Cutler et al. (1990) use what they call a support ratio to highlight changes in production capacity and changes in consumption patterns as the population ages. The support ratio is defined as

a = LF / CON, (1)

where LF is the effective labor force and CON is the effective number of consumers.

Cutler et al. (1990) start by assuming that LF and CON simply are defined as the number in different age groups— that is, an analysis very similar to the analysis discussed earlier called pure demography.

As pointed out in the introduction, aging started with a decline in fertility, which means that the support burden of children lessens. There is a time span before the old age dependency ratio increases; thus, there is a period in which the support burden is lessened. However, in the next phase of the demographic transition, the number of older persons increases, and so does the old age dependency ratio. The per capita consumption demands (needs) from older persons surpass by far that of children. A changing age structure, with fewer children and more older persons, does not have a neutral effect on the support burden. Cutler et al. (1990) therefore qualify the support ratio, taking different consumption patterns in different age groups into account as well as age-specific labor force participation rates.

The support ratio will decline in the decades to come. One of their conclusions is that the support ratio is more sensitive to changing consumption patterns than to changes in the labor force participation rates (see also Erlandsen & Nymoen, 2008).

Aging and the Welfare State

In many countries, a large part of life cycle redistribution takes the form of publicly provided or subsidized consumption and transfers. Division of public expenditure in accordance with the problems the welfare state aims to remedy gives essentially three categories: (1) life cycle redistribution, (2) risk insurance, and (3) what may be called redistribution in accord with our ethical preferences—that is, support of the genuinely weak. A comparison of expenditures in five countries, Britain, Hungary, Italy, Poland, and Sweden, in the middle of the 1990s shows that life cycle redistribution constituted by far the largest part. It ranged from 60% in Britain to more than 80% in Poland. The aid to the weak was the smallest part, below 10% in all the countries except in Britain, where it counted for just above one fifth (Kruse, 1997).

Of course, the importance of life cycle redistribution in the welfare state makes it sensitive to aging. During childhood, the individual is a net receiver of public expenditure; during working ages, a net contributor; and during old age, again a net receiver. During childhood, the main items are education, publicly provided or subsidized child care, and child allowances, to mention a few. During old age, the most important expenditure areas are public pensions, health care, and old age care. With a welfare state model, these expenditures are financed mostly by taxes, which give high tax wedges and are detrimental to employment.

There is widespread concern that population aging will put the welfare state under strain and force a retrenchment. With aging, the tax base decreases if the decline in the number of workers is not compensated for by productivity increases. At the same time, aging increases the demand for pensions, health care, and old age care. Prognoses of these important expenditure areas until the year 2050 are reported, for example, in EU Economic Policy Committee (EU, 2003). Table 57.4 shows these prognoses for a selection of European countries. Per capita expenditure is assumed to be constant; combining per capita expenditure with demographic changes, one gets the following expenditures.

Take health care as an example. The consumption of health care increases strongly with age. Bjorn Lindgren and Carl Hampus Lyttkens (in press) present figures showing the per capita cost for persons aged 80 and older to be around four times the cost for persons aged 30 to 50 years. This figure stems from a simulation model for Sweden. EU (2003) shows an even more marked increase with age. Note that taking this into consideration would change the consumption pattern in the stylized life cycle picture in Figure 57.1. In all the countries in Table 57.4, the number of people in the age group 80 and older will increase rapidly. From 2000 to 2030, the 80 and older share in the population will increase from 4.0% to 9.0% in Italy, from 3.7% to 7.5% in France, and from 3.5% to 7.2% in Germany (United Nations, 2007).

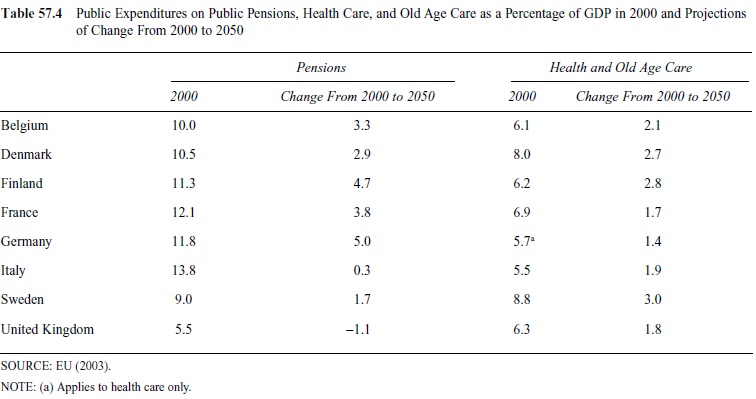Table 57.4 Public Expenditures on Public Pensions, Health Care, and Old Age Care as a Percentage of GDP in 2000 and Projections of Change From 2000 to 2050

To what extent the increased number of elderly people will actually lead to increases in the health care costs is, however, a matter of dispute. Friedrich Breyer and Stefan Felder (2006) report that attempts to foresee the increases in payroll tax rates to cover German health care costs give estimates with range as wide as between 16.5% and 39.5% in 2050. The lower figure stems from simulations using demographic change alone, while the higher one incorporates progress in medical technology, which has shown to be highly cost increasing. Although many technological advances are efficiency enhancing and cost reducing— using medicine instead of surgery for a gastric ulcer, for example—until now it has been cost increasing (see Lindgren & Lyttkens, in press).

It turns out that the effect of aging on health care expenditure is extremely difficult to foresee. First of all, health care has an income-elastic demand, meaning that as income goes up, so does demand for health care. Expenditure on health care closely follows a trend: The higher the GDP, the higher the proportion spent on health care. Thus, at least until now, demography is not the main explanation for increases in spending on health care. Adding costs for increasing quality at the same rate as real wage growth would increase health care costs by a factor of around 3.5% in addition to keeping per capita cost constant up to year 2040 (Lindgren & Lyttkens, in press).

Health care has a greater weight in older people’s utility and demand. Aging means that older people’s influence increases, both as consumers and via the political process as voters. We can thus expect that expenditures on health care will increase and do so more than just in response to demographic change. Furthermore, Richard Disney (2007) shows that aging will be associated with a larger welfare state.

Pensions

In his seminal article, Paul Samuelson (1958) analyzes the problem of how to support oneself in old age. He uses an overlapping generations model with three coliving generations, two working and one retired (children are assumed to belong to the adults’ families and are outside the analysis). To focus on the necessity of cooperation of generations, he assumes that nothing keeps; trade with nature is not possible, and there is no capital market. During the working periods, each person or generation produces one unit.

Samuelson (1958) shows that one way of solving the life cycle problem of smoothing the consumption possibilities, when working capacity does not suffice for all periods, is to make the two working generations pay a percentage of their incomes as a tax and use the revenue for payments to the old generation. One important conclusion from this setup of a contract between generations, a pension system, is that the rate of return on contributions paid equals the population growth rate in the economy. Remember that there is no capital in this economy and thus by assumption no productivity growth. With a positive population growth rate, the number of workers increases; with a fixed contribution rate, the sum of contributions increases, and so do the outgoing payments to the old.

This solves the life cycle problem. However, Samuelson concludes that this kind of system will not come into existence because older persons do not have a negotiatory position to persuade the working generations to accept such a system, nor do they have the power to enforce it because they are in the minority. He points to the fact that life cycle redistribution is a linear business, not a circular one. That is, if A (old) borrows from B (middle-aged) and C (young), A will not be around to repay B in the next period, when B is old and needs support. The solution suggested by Samuelson is a social contact between generations; B gives part of his or her income to A, being convinced that in the period when B is old, C, now being middle-aged, and the new generation, D, now young, will do the same for him or her. In this simple setting, Samuelson shows the workings of a pay-as-you-go pension system and also that the rate of return in such a system equals the growth rate in the economy.

All industrialized countries have public pensions systems, often supplemented with pensions negotiated between the parties in the labor market and with private pensions. In most countries, public pensions provide the major part of income during retirement and constitute a large part of public sector expenditure. These expenditures are forecast to increase substantially with aging; hence, reforming the existing pension systems has become a top priority on political agendas.

Old age pensions can be organized in a number of ways. The main choices to make are the following:

Public or private
Obligatory or voluntary
Pay-as-you-go or funded
Defined benefit or defined contribution
Basic or earnings related
Redistribution or actuarial
Indexed with prices, growth, or interest rate (rate of return in the capital market) during contribution years and during benefit receiving years.

The specific design chosen has different effects on the distribution between generations, on the rate of return the system gives, and also on how robust the system will be in response to demographic changes.

Public pensions are more often than not obligatory, meaning that the individual is not free to choose a life cycle consumption pattern according to his or her preferences. If the restriction imposed by the pension system is binding, this means a loss in utility. The higher the level of the system, the higher the probability of a binding restriction, which is probably more binding in low-income groups than in high-income groups. The reasons put forward to justify an obligatory system and this loss are the threat of free riders, the fear of myopia among younger people, and the desire to use the pension system for redistribution among socioeconomic groups.

A pay-as-you-go system may be described by its budget restriction:

q x w x L = b x R, (2)

where q is the contribution rate, w is the average wage, L is the labor force, b is the average benefit, and R is the number of retirees. The left-hand side shows the sum of contributions (in a time period, a year, for example) and the right-hand side shows outgoing expenditures in that same period—that is, to contemporary retirees. The character of a pay-as-you-go system to be an implicit social contract between generations becomes evident with this formulation.

For the system to be in balance, the equality sign has to hold. Assume that wages, the labor force, and the number of retirees are exogenous to the pension system. It is then obvious that with demographic changes like those expected in the future, either the contribution rate has to be increased or the benefit level decreased, or both, in order to maintain a balanced system.

Rearranging equation 2 shows even more lucidly the importance of demography in a pay-as-you-go system:

q = b/w x R/L, (3)

where b/w is the replacement rate—that is, the benefit in relation to wages—and R/L is the dependency ratio.

Table 57.5 is to be read in the following way: With a dependency ratio, R/L, of 0.33, a contribution rate of 16.5% suffices for a replacement rate of 50%. If a higher replacement rate is wanted, for example 60%, then a contribution rate of 20% is needed. The combined information in Tables 57.3 and 57.5 leaves no doubt that aging will lead to pressure on pay-as-you-go pension systems.

The budget restriction shows the working of a pay-as-you-go system from society’s point of view, but it can also be used to show it from an individual’s life cycle perspective as well. With such a perspective, L may be seen as the number of years the individual works, say from 20 to 64 years of age, giving 45 working years. R is then the number of years in retirement, say from 65 to 80 years of age. Using these figures in equation 3 gives

q = b/w x 15/45. (4)

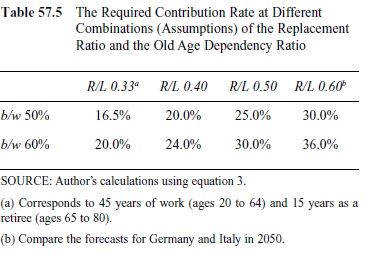Table 57.5 The Required Contribution Rate at Different Combinations (Assumptions) of the Replacement Ratio and the Old Age Dependency Ratio

Assume that the individual wants a replacement rate of 60%. It is then obvious that the contribution rate has to be 20% (see also Table 57.5). The equation can be used to illustrate different changes. Assume, for example, that the individual wants to retire earlier, other things being equal, at 60 years of age. Then we get

q = b/w x 20/40, (5)

with a replacement rate, b/w, of 60%, the contribution rate has to be increased to 30%. Evidently early retirement is very expensive.

A last example here is increases in longevity. Assume an increase of 5 years, other things being equal. This gives us

q = b/w x 20/45. (6)

Again, with a b/w of 60%, the contribution rate to balance the system is 27%.

The effects of aging on pay-as-you-go systems made policy makers and pension experts recommend reforms to change from pay-as-you-go systems to funded ones (see, e.g., World Bank, 1994).

In a funded system, the contributions paid during working years are put into a fund, which may invest in the stock market or hold equities, government bonds, or both. The fund increases each year with new contributions and with compound interest earned by the fund. At the time of retirement, the fund can be used for buying an annuity, the size of which depends of course on its value at the time of retirement.

There are pros and cons with either way of organizing a pension system. Obviously, the rate of return differs; in a pay-as-you-go system, it equals (approximately) the economic growth rate, and in a funded system, it equals the rate of return in the capital market. Historically, and in the long run, the rate of return in the capital market has surpassed the growth rate. This led Martin Feldstein (1974), among others, to the conclusion that funded systems were to be preferred; the same benefit would be possible with lower contribution rates. Thus, both aging and an expected discrepancy between growth and the interest rate seem to favor a funded system. Feldstein’s conclusion builds, however, on the assumption that funding—and the eventual increased capital supply—will not affect the rate of return. If a great number of countries were to follow the advice of transforming their pay-as-you-go systems into funded ones, it is hard to believe that there would not be a downward pressure on the interest rate. Furthermore, it is worth noting that funded systems, to a certain extent, are also sensitive to demographic changes; for example, with a funded system, when baby boomers enter retirement and sell their funds to buy annuities and the increased capital supply meets a smaller working generation, the price—that is, the rate of return—will most certainly go down. Axel

Borsch-Supan, Alexander Ludwig, and Joachim Winter (2006) show that demographic effect on the rate of return depends on the degree of funding as well as on the degree on international openness in the capital market.

It should be noted that both kinds of pension systems are exposed to risk; a pay-as-you-go system is exposed to the risk of a deteriorating economic performance and low growth, and a funded one is exposed to the risk of capital market crises. Thus, it may be a good idea to diversify, to use both devices.

Whether pay-as-you-go or funded, pensions are mainly life cycle savings with a smaller part being insurance. The insurance is in order to cover an extraordinarily long life— that is, the risk of outliving one’s means. Insurance uses the law of large numbers, meaning that it is enough to have a buffer (savings) covering the average expected number of years as a retiree. With insurance, the risk of living longer than average life expectancy is pooled among the participants in the pension scheme. Because individuals have risk aversion, without insurance, the individuals would keep a too large buffer, which reduces expected utility.

The budget restriction of a pay-as-you-go system clarifies the difference between a defined-benefit (DB) and a defined-contribution (DC) system. In a DB system, the benefit (b) or the replacement rate (b/w) is fixed. Demographic and economic changes then have to be counterbalanced by changes in the contribution rate (q) in order to keep the system in balance. This means that the costs of adaptation to these changes fall on the working generation. As this discussion has shown, aging leads to a shrinking labor force; in a DB system, this requires raised contribution rates. In a DC system, the contribution rate is fixed and benefits are then determined by the sum of contributions divided by the number of retirees. Aging, in the form of increased life expectancy, means that yearly benefits decrease in proportion to the increase in the number of years as a retiree. In the last decade, there has been a trend away from DB to DC systems, indicating a shift in who bears the risk of increased life expectancy, from the working generation to the retired one (Whitehouse, 2007).

The natural index in a pay-as-you-go system is the growth rate (again, see Samuelson, 1958). However, many countries have chosen to index by prices, the reasons often stated to be economic. This implies, though, that the development of the pension system does not follow the development of the economy and will thus be exposed to economic changes because it does not adapt automatically. The standard of living of different generations will be determined by economic growth; with a high economic growth, the retirees’ standard of living falls behind that of the working generation, and vice versa.

In an actuarial system, there is no redistribution ex ante. The sum of expected contributions equals the sum of expected benefits. Of course, there will be redistribution ex post; some people will end up as losers, living shorter than the expected average, and some as winners. If there are no systematic differences between people or socioeconomic groups, then the system is actuarial. Note that if unisex life tables are used, there is redistribution in favor of women. In an actuarial system, with the contribution rate determined as a percentage of the wage, the system will be earnings related. Because women have a different labor market performance from men, with market work interrupted for child rearing, earnings-related systems are sometimes assumed to be disadvantageous to women. However, this turns out not to hold generally; see Ann-Charlotte Stahlberg, Agneta Kruse, and Annika Sunden (2005) for an analysis of gender and the design of pension systems.

The Political Economy of Public Pensions and Aging

Edgar Browning (1975) shows that in a democracy with majority voting, a pay-as-you-go system will expand beyond its optimal level. To show this, he uses an overlapping generations model with three generations, one young, one middle-aged, and one old. The young and middle-aged are working, earning yy and ym respectively. To introduce a pay-as-you-go system, they all vote on their most preferred tax or contribution level, knowing that the sum of contributions paid into the system is to be used for benefits to the contemporary old generation. The voters assume that the tax rate will not be changed in their lifetime.

Assume that the individuals maximize their lifetime utility. The old individual has only one remaining period left to live. This period is spent in retirement; the old person will not pay any contributions but will receive benefits. At the extreme—for example, neither taking the utility of children and grandchildren into account nor expecting negative incentive effects—the old person will vote for a tax and contribution rate of 100%, told. The young individual has his or her entire life ahead of him or her and will pay contributions during a whole working life and get benefits during retirement. The preferred contribution rate by the young will smooth the consumption path over the life cycle, maximizing utility. The young person’s chosen contribution rate is thus the optimal one, t*, as the entire life is taken into consideration. The middle-aged generation’s most preferred tax rate will be between the old person’s and the young person’s. What the middle-aged generation has left is one period of working and contributing to the system and one period of getting benefits: t* < tmiddle~aged < told . With majority voting, the median voter casts the decisive vote, and the system will be greater than its optimal level. The outcome builds on rather simplified assumptions, for example, that the only aspect of voting is the level of the system and that voting takes place only once. Other researchers have qualified the Browning model and made assumptions closer to actual pension systems and more realistic voting procedures; even so, the Browning result holds well (see, e.g., Sjoblom, 1985).

This result is even reinforced by aging. Aging means that the age of the median voter increases. By the turn of this century, the age of the median voter was well below 50 years of age; in 35 years, it will increase to 54 in Germany, 55 in Italy and Spain, and 56 in France, to mention a few countries with rapidly aging populations (Galasso, 2006; Uebelmesser, 2004). Figure 57.2 shows how the median voter’s considerations change with increased age.

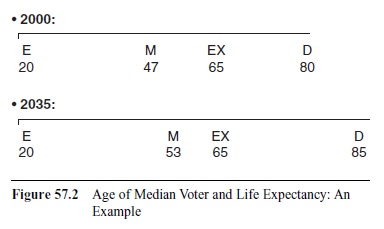Figure 57.2 Age of Median Voter and Life Expectancy: An Example

Assume that voting takes place in the year 2000 and that the median age is 47, retirement age 65, and expected remaining lifetime 15 years. Contributions before the age of 47 are sunk costs. The median voter knows that he or she has another 18 years of contributions (compared to the 40 to 45 years a person entering the labor market has) and 15 years of benefits. It is assumed that the median voter’s age has increased 35 years later to 53 years, the retirement age is the same, but the expected lifetime has increased by 5 years. Voting in 2035, the median voter now has 12 years of contributions and is expected to get benefits during 20 years. A high contribution rate will certainly give a high payoff.

Aging gives rise to an opposite effect as well by exerting a downward pressure on the growth rate in the economy—that is, a downward pressure on the rate of return in a pay-as-you-go system. Therefore, it may be attractive to downscale the pay-as-you-go system and replace it with a funded one. So far, according to empirical results, the former tendency seems to have been the stronger:

The most striking result… lies in the strong and significant positive effect of median voter age on program size. … one year adds half a percentage point to the GNP share of social security benefits. (Breyer & Craig, 1997, p. 719)

This also implies that reforming a pension system in response to the strain aging puts on the systems is politically difficult. Reform efforts have been met with fierce political resistance, especially from the so-called gray panthers. This notwithstanding, there has been a plethora of reforms in a number of countries where aging has put the pension systems under strain. The reforms range from marginal retrenching changes to radical parametric ones (Galasso 2006; Martin & Whitehouse, 2008). Radical reforms are of course more difficult to accomplish. HansWerner Sinn and Silke Uebelmesser (2002) analyze the political possibilities of such a change in the German system and conclude that it will be possible until around 2015. After that date, Germany will turn into a gerontocracy, and such a change will not be politically feasible.

In Sweden, a radical reform was decided on in the middle of the 1990s. The system was changed from a DB to a DC system—the major part being kept as a pay-as-you-go system and a minor part transformed to a funded one— from price indexation to (in the main) wage indexation and with annuities depending on life expectancy. It is regarded as being a stable pension system despite the aging of the population (for a description see Kruse, in press; Palmer, 2006). Jan Selen and Ann-Charlotte Stahlberg (2007) and Kruse conclude that the design of the transition rules was a crucial factor to form a majority in favor of the new system, together with high political competence. Other countries as well have implemented more or less similar reforms. Robert Holzmann and Edward Palmer (2006) thoroughly describe and analyze the pros and cons of these reforms.

Possible Remedies and Concluding Remarks

There is no doubt, first, that aging will occur with increased old age dependency ratios, and second that aging will affect the extent of resources channeled to the elderly as well as affecting the possibilities of financing these resources. The prognoses give an increasing gap between available resources and future demands due to aging, ceteris paribus. Furthermore, aging is not the only foreseen challenge; in combination with ongoing globalization, aging is supposed to increase the strain. However, the ceteris paribus assumption will not come true. If there is anything to learn from history, it is that economies are flexible, adapting to new circumstances. The adaptation may, however, be costly.

To close the gap between the increasing demands due to an increased number of older persons and decreasing support possibilities due to a shrinking workforce, a number of measures aiming at both the demand and the supply side will probably be called for.

Immigration is often suggested as a remedy against the decreasing number of people of working age. However, demographers show convincingly that immigration is not a remedy; see for example Tommy Bengtsson and Kirk Scott (in press). Calculations show that the amount of immigration needed in order to compensate for demographic change and aging by far surpasses what is deemed possible to accommodate. Furthermore, even if the only accepted immigration would be people in working ages, immigrants also eventually get old and needy. Besides, such immigration assumes a rather odd immigration policy.

Another possibility would be to increase fertility, for example by stimulating fertility by subsidizing child rearing, making it possible to combine market work and children. Such policies are assumed to have kept fertility rates at rather high levels in France and Sweden, for example, in comparison with Germany, Italy, and Spain. However, fertility seems to be difficult both to predict and to influence. Besides, more children will at least initially not diminish the gap. On the contrary, it will reduce market labor sup-ply because time is an important input into child rearing.

To raise taxes would be another way to close the gap. However, taxes give rise to incentive effects, which may reduce the tax base and cause deadweight losses. The deadweight loss increases with the square of the increase in the tax rate, making it an expensive way to go. There are, however, tendencies of a reformed tax structure, much in response to globalization, but it may also facilitate the financing of the welfare state (Bergh, 2008; Hansson, in press). Examples are pension reforms with a tighter connection between contributions and benefits, for example in the French and German point systems and in the Swedish defined-contribution system. The Japanese and German old age care insurance systems are other examples. Such earmarked taxes reduce the distortive effect of a tax.

An increased labor supply seems to be many countries’ most favored measure to meet the strain of aging. For a long time, the opposite was common, with a number of countries taking measures to facilitate early retirement (see Gruber & Wise, 1999). To meet the challenges of aging, a number of countries are now trying to reverse these measures. Mandatory retirement ages are increased, and ways for early exit have been closed. Again, a closer link between taxes or contributions and benefits gives incentives for working longer hours and postponing retirement. Increased labor supply may be the solution to the financing problem caused by aging. Policy measures to give incentives in this direction are thus called for.