Traditional Teacher Tests Research Paper

This sample Traditional Teacher Tests Research Paper is published for educational and informational purposes only. Like other free research paper examples, it is not a custom research paper. If you need help writing your assignment, please use our custom writing services and buy a paper on any of the education research paper topics.

All students experience various classroom assessments, ranging from pop quizzes to essays to traditional multiple-choice tests. Undoubtedly, there has been some time in your life when you questioned the fairness of a classroom test. Unfortunately, some teachers likely proceed with assessments and interpretations without giving student complaints legitimate credence and use that same assessment the following year. This does not describe all classroom testing experiences, but most of us can recall at least one experience where this scenario rings true.

Reasons for this situation include: (1) lack of sufficient training in constructing tests in teacher preparation programs, and (2) a mismatch between educational measurement theory and practice on the proper construction of teacher-made tests. Also, research is more focused on construction and interpretation of standardized tests, even though they have little direct application in classrooms— standardized test results are not received in a timely enough manner to directly affect instruction, making it difficult for teachers to apply standardized test results in their teaching.

Despite the insufficient focus on teacher-made tests in teacher education programs, it is important for teachers to have the knowledge and skills to construct and use traditional classroom tests. This research-paper discusses the properties and importance of traditional teacher-made objective tests in classroom settings. The effects of increased employment of high-stakes standardized tests on the use of traditional classroom tests in a standards-based era also are discussed.

Need for Assessment

As Horace Mann is deemed the father of American education, so too is Ralph Tyler the father of curriculum and instruction. Tyler’s book, Basic Principles of Curriculum and Instruction (1949), played a seminal role in reforming the then current state of instructional practices. Tyler called for a focus on educational objectives that were to be planned, taught, and evaluated. Until that point there were no real measures of accountability of learning in place. After Tyler, evaluation of objectives became a fundamental component to ensuring that desired student learning was being achieved. Subsequently, objectives became the basis of classroom assessment. Benjamin Bloom’s, Taxonomy of Educational Objectives (1954) provided educators a way to classify learning and assessment tasks for years to come. Objectives are the key ingredients to making the planning, instructional, and evaluation of phases of instruction flow together.

Overview of Teacher-Made Tests

Standardized Versus Nonstandardized

There are two major categories of tests: standardized and nonstandardized. Standardized tests are administered and scored using fairly uniform standards. They can be used to make either norm-referenced (relative comparisons)  or criterion-referenced  (absolute comparisons)

interpretations of student learning. Until the No Child Left Behind Act of 2001, many standardized tests were used to make norm-referenced interpretations of student learning. Currently, 45 states administer a criterion-referenced state standardized test (Education Week, 2007); however, to reiterate, test results are rarely returned in a timely manner, thus minimizing the potential instructional effect.

Nonstandardized tests, or teacher-made tests, are exactly that—tests constructed by individual teachers. There are no standardized procedures in construction, administration, or scoring. Most student assessment exists in the form of classroom-level tests. Historically, traditional teacher-made objective summative tests, or tests used at the completion of learning, composed typical testing practice.

Teacher-made tests can be used for either criterion- or norm-referencing; however, Black and William (1998a) reported that teachers tend to make norm-referenced (i.e., social comparative) interpretations. Criterion-referenced interpretations, however, are more appropriate: students can perform a certain skill regardless of how others perform.

Prevalence

Stiggins and Bridgeford (1985) found that the majority of teachers reportedly use teacher-made tests and that use increased with grade level: 69% of second-grade teachers versus 89% of eleventh-grade teachers. Most teachers (75%) reported having some concern about their own tests; higher grade level teachers were most concerned about improving them.

McMillan and Workman (1998) reported that many teachers assess basic facts, knowledge, and rules; use short-answer or objective test questions (Frary, Cross, & Weber, 1993); have difficulty with constructing higher-order thinking questions; and have low levels of competency regarding classroom assessment, specifically communicating results. McMillan (2001) found that secondary teachers reported using their own assessments (98%) more frequently than prepackaged assessments (80%). It is unclear whether these assessments were objective or performance-based. Although older studies indicate that formal tests occupy 5 to 15% of students’ time, more recent figures are unavailable (Crooks, 1988).

Teacher Perspectives

Teachers perceive teacher-made tests as important. They view their use of traditional tests in high regard (Pigge & Marso, 1993) and put more weight on teacher-made tests (versus other assessment methods) when assigning final grades (Boothroyd, McMorris, & Pruzek, 1992). Despite the high frequency of reported use, teachers tend to be quite independent and somewhat reluctant to share ideas in developing and using their tests (Cizek, Fitzgerald, & Rachor, 1996).

Much research indicates that some teachers lack the sufficient competency in measurement and assessment necessary to justify how test results are currently used (Stiggins & Bridgeford, 1985; Boothroyd, McMorris, & Pruzek, 1992). This may be because preservice teachers perceive courses that focus on traditional teacher tests and measurement as less valuable than those that focus on alternative assessment methods (Taylor & Nolen, 1996).

Prepackaged Tests

Teachers now commonly use tests that are included in prepackaged programs or textbooks. Most comprehensive school reform programs, textbooks, and many curriculum programs now come with ready-made assessments.

Teachers are busy and some readily welcome prepackaged tests with open arms. They provide quick access to assessments and given what research has shown about teacher competency in test construction, it is understandable that teachers use these tests with too little concern. Prepackaged tests, however, are not a panacea for improving student learning. Prepackaged tests are developed for a general student under general learning circumstances. McMillan (2007) points out three key points regarding the use of published tests:

1. A textbook’s or curriculum program’s text does not ensure high quality. Similarly, many tests are accessible via organizational or peer collaboration Web sites. Teachers need to assess the quality of any test they encounter.
2. Tests of high quality do not necessarily measure the learning outcomes intended by a teacher. Not all textbooks align with teachers’ learning objectives, especially under the No Child Left Behind Act. This is because local education agencies have had difficulty adopting textbooks that align with their state’s standards.
3. The language and presentation of concepts on tests that publishers use may differ from that used by the teacher. Instruction and assessment must be aligned.

Nevertheless, teachers can modify prepackaged tests. It will take more effort and time than just using the commercial test, but the instructional gain may prove to be higher than just accepting the status quo. The advantage of a teacher-made test or modified commercial test over a prepackaged test is the ability to adapt to a local environment (e.g., different learning abilities, cultural backgrounds, and so forth) to ensure that test results are used appropriately.

Instructional Importance

Two commonly reported uses of teacher-made tests are for grading and reporting and for diagnosing learning difficulties (these topics will be discussed later). Tests serve other important functions such as allowing teachers to make accurate instructional decisions, determining student’s prior knowledge, and determining the effectiveness of instruction.

Tests can be used both formatively and summatively to help assess student learning. It is common practice to use tests in a summative fashion—at the end of instruction as an assessment of learning, rather than during instruction as an assessment for learning. Black and William (1998b) contend that effective implementation of formative assessment can raise educational standards and is an important aspect of effective teaching because the teacher focuses on higher-order thinking and less on grades, administers many assessments, and provides high-quality feedback. It also allows for learning to occur on an individual level. Paper-pencil tests play an important role in formative assessment—they help teachers gauge learning and modify instruction.

Tests should focus on both higher and lower cognitions of learning—not just rote memorization—and be shared with colleagues. Often there is a disconnect between teachers’ instructional intent and the assessments they choose to measure learning. When tests align with developing a deeper understanding, their utility becomes greater.

One way of ensuring that instruction aligns with assessment is to use a test blueprint (table of specifications). Just as an architect builds a building from a blueprint, a teacher can use a blueprint to build tests. Blueprints allow teachers to make sure that the learning objectives from a unit are assessed on the test at appropriate levels of cognition (see Figure 47.1). Typically, blueprints use Bloom’s original (Bloom, 1954) or revised taxonomy (Anderson & Krath-wohl, 2001), but any cognitive taxonomy can be used. Recommendations for creating test blueprints can and ought to be modified to meet teachers’ needs. Another valuable feature that can be added to blueprints is item types, which can help teachers gauge how much time the test will take.

Using Assessment Results

Part of using teacher-made tests to their fullest extent is using the results appropriately and efficiently. Simply returning test scores to students is not nearly enough to enhance learning. If anything, it creates higher anxiety for students because it puts more emphasis on the grade rather than on comprehension. If teachers construct high-quality tests, provide high-quality corrective feedback, and reassess, then students will experience positive assessment experiences.

Consider Situation 1.

Situation 1:

Anne received a 72 on a quiz on multiplication facts. The only feedback on the quiz was the grade and which items she got wrong. The teacher proceeded with the unit on converting percentages to simplified fractions. On the unit test, Anne received a 69.4, where again the feedback only indicated which items she got wrong. Since the teacher rounded Anne’s score up to a 70, Anne was satisfied with her grade and the teacher moved on to the next unit.

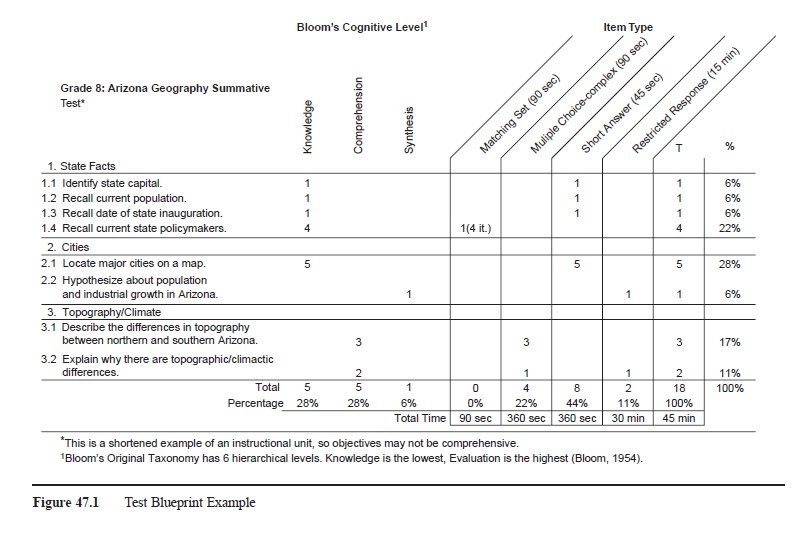Figure 47.1    Test Blueprint Example

The teacher in Situation 1 failed to provide Anne with proper corrective feedback and remedial action. The quiz only provided indication of performance and offered no direction for Anne to focus her learning. The teacher should have given Anne feedback about what specifically she got wrong on the test and some direction to the right answer. In addition, before the unit test, the teacher should have given Anne additional assessments (homework, work sheets, quizzes, oral questioning, etc.) to ensure that she clarified the problems she had with multiplication facts. Similar situations can interfere with students’ motivation to learn and promote a focus on not failing rather than on achieving mastery (authentic and higher-level understanding).

Understanding that one score is just one measure of an entire domain of measurements to be taken and that the inferences drawn about student learning must be appropriate given the nature of the test are also important concepts for teachers to know.

Data Analysis and Tracking

Teachers do not need to be statisticians to do analyses on student achievement data. Many statistical tools are available through programs that are likely already available to them. Simple statistics (e.g., mean, median, mode, and range) provide great insight to the quality of instruction and learning, as do more advanced statistics (e.g., standard deviation and correlation). Tracking student, class, and even grade-level trends serves great instructional purposes for teachers.

Tracking longitudinal student trends on various concepts can assist teachers in seeing individual strengths, weaknesses, improvements, and so forth. When teachers have a better grasp on students’ learning difficulties, they can provide precise remedial work. Data analysis of teacher-made test data can also help teachers over the years determine which concepts are difficult to teach. For these problematic areas, teachers can modify instruction and administer the same tests both before and after instruction to help ascertain mastery of learning.

Collaborating with colleagues and devising grade-level analysis procedures can also provide great insight regarding students’ performance and can help create uniform interpretations within a school. Additionally, visual data analysis is an informal yet useful method for interpreting results. Teachers can construct simple charts and graphs to get a better grasp of student performance.

For example, Table 47.1 shows five math test scores for three students from the first quarter of school. Based on the means alone, which is a common practice, one would conclude that all three table 47.1 students performed about the same; however, the range and trend of scores is very different. Figure 47.2 visually displays the longitudinal trend of scores. These results can help the teacher see that Bill made great improvement, Mike’s performance declined, and John performed about the same on all five tests. If the teacher regularly looked at trends in student data, after Test 3, the teacher could have looked into why Mike’s test scores have been decreasing and made appropriate instructional decisions.

Data analysis can also be used at the class level. Figure 47.3 displays a histogram (frequency count) of the Test 1 scores of a class (10 students). Using this graph the teacher can obtain a better estimate of how the class did as a whole. The mean was 84.8. When combined with Table 47.1, the teacher can see that John scored near the average on Test 1, Bill scored below average, and Mike scored above average. These norm-referenced comparisons should not drive instructional decisions, but they do provide additional insight to student performance. If the class mean was lower than 84, maybe 65 or 69, this would alert the teacher to inadequate instruction of content or a poorly constructed test, or perhaps the students did not study.

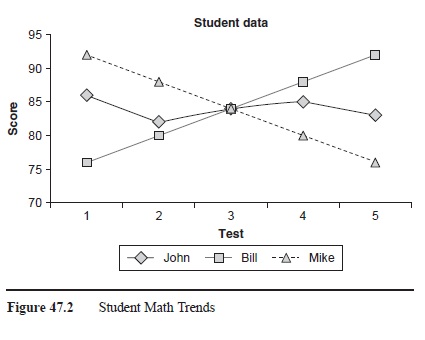Figure 47.2      Student Math Trends

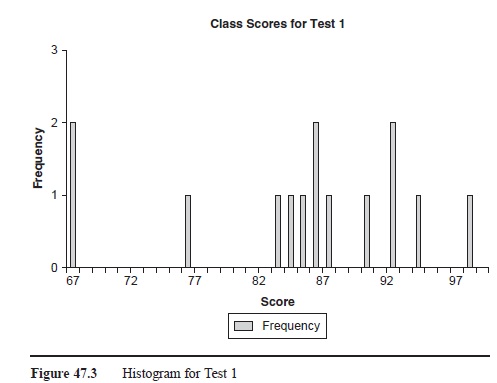Figure 47.3      Histogram for Test 1

Measurement Theory Versus Classroom Application

Teachers must be concerned with reliability and validity of their assessments. There is, however, much debate regarding to what extent classroom tests should possess certain technical properties and the types of statistical computations teachers ought to perform. In almost any classroom assessment textbook there is some mention of reliability and validity of assessment of learning. Some textbooks are very detailed and offer exact calculations of various types of reliability and validity evidence (Nitko, 2004); some are focused less on the numerical properties and more on conceptual understanding (Popham, 2005).

The biggest obstacle preventing teachers’ comprehension and application of reliability and validity is the mismatch between educational measurement theory and actual classroom processes. A strict focus on measurement theory tends to dehumanize and threaten the very essence of teacher-student relationships. It is difficult for teachers to think of student learning only in numerical terms, and there is no reason why they should. Teachers ought to be concerned about the effects of any assessment on student motivation and emotion. It is therefore beneficial to present the topics of reliability and validity in ways similar to how teachers ought to think—from a student’s perspective.

Reliability

Reliability is how consistent or stable assessment results are, or that results from a given assessment will generalize to later conditions; scores will yield similar results across different time periods, different forms of a test, or both. Calculating reliability coefficients can be an arduous task that teachers may not benefit much from, have the statistical expertise to do, or most important, have the time to do.

Measurement Error

Rather  than  calculating coefficients, teachers ought to be aware of the importance of the concepts of reliability and how they can help improve assessment of student learning. When assessing students, consistency is important. Teachers want to be able to say confidently that student test scores are not a function of measurement error, or unpredictable error. Measurement error is the error associated with the act of measuring a certain attribute and is essentially the heart of reliability. A common example is a weight scale. Often, different weights are yielded on different scales and at different times. One may weigh more at night than in the morning; or weigh more on a cheap scale in the bathroom than on the expensive scale at the gym; or may get on the scale, get off, then get right back on and read two completely different measurements. Regardless, if off by 1 pound or 20, it is still an inconsistent measurement—some sort of error makes the observed weight not equal the true weight had there been no error. The problem is that there is error in all measurements—elimination of error is impossible. True measures of certain attributes can never be obtained; instead, estimates are the best measures that can be produced and we hope that the observed measurement is as close to the true as possible. Essentially, the goal is to reduce error as much as possible.

Practical Applications

This notion of error is very useful when assessing students. It is very common for educators, policy makers, parents, and students to take a single test score and make highly significant inferences based on that one score, not realizing that it is just one measure of student achievement. For example, consider the following situations.

Situation 2:

Johnny received an 83 on Mrs. Smith’s geology test taken on Monday. Johnny takes the same test on Friday and receives a 95. Mrs. Smith is quite perplexed and after inquiry finds out that on Sunday night Johnny was ill and only slept for 2 hours.

OR

Situation 3:

Johnny received an 83 on Mrs. Smith’s geology test taken on Monday. Johnny took the same test on Friday and received a 66. Come to find out Johnny really did not study for the test on Monday and so guessed on the majority of the answers.

Often, teachers do not give the same test twice and so in Situation 2, Johnny’s true geological performance would be underestimated and in Situation 3 it would be overestimated. Eliminate the Friday test and Johnny would undoubtedly have no complaints in Situation 3, but be very upset in Situation 2, and either way Mrs. Smith would be ignorant of Johnny’s true performance.

Consider a different example.

Situation 4:

Mrs. Smith administered a geology test on Monday. Her daughter was ill all weekend long, so she did not have time until 1 a.m. Monday morning to construct the test Consequently, the test was prone to error, confusing directions, and nonsensical items. The class average on the test was 72. Johnny was sick the first 3 days of the week, so missed the exam. Mrs. Smith allowed him to take a make-up on Friday and had ample time to construct a new test. Johnny scored a 92, and she concludes that his knowledge of geology is well above that of the class.

Situation 4 is exemplary of how test construction error can affect consistency of scores. It is very likely that the rest of the class would score higher had they taken the make-up test with Johnny. In this case, the error within the test itself gives Mrs. Smith less certainty that the results are indicative of students’ true performance levels. This situation is also exemplary of how error can affect validity, which will be discussed in the following section. Think of a test as a scale—the score will vary depending on the conditions surrounding the measurement. The higher quality the scale, or test, used to take the measurement, the greater the likelihood that the observed measurement will be closer to the true measurement.

These sources of error contribute to the dependability of scores, thus influencing the inferences drawn about test performance, which is why educators would be remiss to not consider them. Although there are statistical ways to estimate reliability, often the assumptions of large sample size and large variation in scores are not met at the classroom level. After all, teachers ultimately do not want a wide range of scores; they desire all students to do well. Therefore, a conceptual approach is more appropriate.

Validity

Validity is the accuracy of the inferences and uses of test results. Where reliability is concerned with consistency and generalizability of results, validity is concerned with whether tests actually measure what they are purported to measure and whether the use of any test is appropriate. Similar to reliability coefficients, validity coefficients can also be calculated and are subject to the same concerns.

From a students’ perspective, validity is about fairness. When students interpret a test as being an unfair measure of achievement, the validity of the interpretation of results is often undermined. Reconsider Situation 4. Because the test was so error-prone, it is erroneous for Mrs. Smith to conclude that Johnny performed well above the class. In this case, Mrs. Smith is drawing an invalid inference about students’ geological achievement. Most of the students who took the test on Monday will perceive the test to be an unfair assessment of their true achievement; instead of measuring geological achievement, the test measures other irrelevant factors.

It is important to note that fairness is not the same across all students: what some students consider fair, may be considered unfair by others. For example, some students may have trouble concentrating in the middle of the day or after lunch. Some may be easily affected by outside disturbances, and some may simply not test well, but do possess content knowledge. All of these situations affect the validity of test results, but it is the teacher’s responsibility to detect and adjust these difficulties as warranted. Teachers need to determine to what extent different perceptions of unfairness affect student assessment, and diagnose and treat the problems accordingly.

Systematic Error

As with reliability, it is easier to make the argument that teachers ought to be more concerned with logically applying the concept of validity and less concerned with the statistical application. Where reliability is concerned with unpredictable error, validity is concerned with systematic error, or predictable error. Systematic error affects the accuracy of the measure, not the consistency. Referring to the scale example, consider that one is using a very high-quality scale (Olympic quality), but calibrated the scale incorrectly (the zero point starts at the 2 pound mark). Every time a measurement is taken it will consistently be off by 2 pounds. In this case, the error is not unpredictable as in reliability; rather it is completely predictable—consistent but inaccurate measurements are taken. This is a key concept in understanding reliability and validity: reliability is a necessary but not sufficient condition for validity—something can be reliable without being valid, but to be valid, it must be reliable.

Practical Applications

Showing evidence of validity is not always as simple as a mere statistic. One type of evidence for validity is showing that one’s content is both representative and relevant to stated learning goals. This is something that teachers need to do. Tests should include items that are representative and relevant to instruction, regarding both content and level of cognitive demand. For example, if the instructional unit covered spelling U.S. cities and the test included items that covered locating U.S. cities, it would invalidate the use of the assessment results, especially if there are high-stakes inferences drawn about student ability to spell U.S. cities. Similarly, given the same instructional unit, if the test included only one U.S. city to spell, that too would invalidate the use of results. The sample of test items was not large enough to make an appropriate inference about students’ ability to spell U.S. cities.

A test blueprint, as noted, is a great tool for ensuring that tests are aligned with instruction, specifically for the longer summative unit or research-paper tests. This visually allows the teacher to see what objectives are being measured, by how many and what types of items. A more informal method of checking for evidence of validity is to have colleagues familiar with the content review the test.

It is important that educators are able to assert confidently that students’ performance on a test reflects the interpretations being made. Being cognizant of intended learning goals, test content, and test development and scoring procedures helps prevent invalid inferences from being drawn.

Standards for Proper Test Construction

The Code of Professional Responsibility in Educational Measurement (National Council on Measurement in Education [NCME], 1995) and the Standards for Teacher Competence in Educational Assessment of Students (STCEAS; American Federation of Teachers, National Council on Measurement in Education, & National Education Association, 1990) are intended to provide educators support in the development of fair and high-quality tests. The main standards in the STCEAS are that teachers should be skilled in (1) choosing and developing appropriate assessments; (2) administering, scoring, and interpreting results from both published and teacher-made tests; (3) using assessment results when making instructional decisions; (4) developing valid grading procedures;

(5) communicating assessment results to others; and

(6) recognizing unethical and inappropriate uses of assessment results.

Types of Tests

There are two common forms of paper-pencil tests that teachers make: constructed response and selected response. Constructed response items include essay items and short-answer or fill-in-the-blank items (FIB). Selected response items include multiple-choice, matching, and true/false items. Teachers report using short-answer and multiple-choice tests with the most frequency (Frary, Cross, & Weber, 1993); however, in some subjects like language arts, essay questions are used more frequently. See Table 47.2 for strengths and limitations of various item formats.

Constructed Response

Essay tests are very common in subjects like language arts, literature, and social studies, where synthesis and organization of ideas or other higher-order thinking skills  (HOTS) are more important than lower levels of learning. Although short-answer and fill-in-the-blank questions are considered constructed response items, they are typically more objective than essays and require students to write a one- or two-worded response.

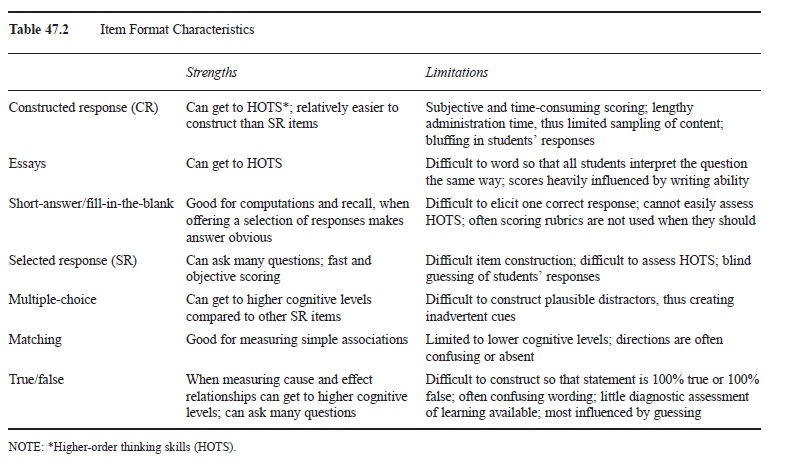Table 47.2       Item Format Characteristics

Selected Response

Multiple-choice (MC) items are the most common item format among classroom teachers. Matching items provide a fast and efficient way for measuring simple associations (e.g., books and their authors, people and their birthdays, and so forth). True/false items involve a binary categorization of any given statement and come in varying formats: right/wrong, correct/incorrect, fact/opinion, etc.

Combining Formats

It is quite common for teachers to include multiple item formats on a single test. So long as careful attention is given to test construction and layout, this allows teachers to assess learning in a variety of ways and at cognitive levels ranging from simple recall to synthesis and evaluation of concepts. When this is done, however, extended essays are often not used due to time constraints. Rather, restricted-response essays (usually one to two paragraphs) are used in conjunction with some combination of selected response item types.

Writing Quality Tests

As discussed earlier, being equipped with the knowledge and skills to construct high-quality tests is desired not only so that one can administer high-quality assessments, but also so that one can assess the quality and appropriateness of prepackaged tests. The previously discussed assessment standards provide general guidelines for proper assessment use, but the question of how to actually write quality tests still remains.

Guidelines

Situation 5:

Sue and Joe Just took a Civil War test in Mr. Clark’s class. They discuss how they think they did during lunch. By the time their conversation is over, they have summed up the following complaints:

• Items 4 and 7 had two correct answers.
• Sue thought she could reuse the responses on the matching set and Joe thought he couldn’t.
• Item 10 was offensive to Joe because his great-greatgrandfather was a slave owner.
• Item 12 used a word that neither knew.
• Both figured out that the answer to item 5 was in item 8.
• Items 6 and 9 were never covered in class.

Unfortunately, Situation 5 is a far too common occurrence in classroom testing. Poorly constructed tests, similar to that in Situation 5, affect students’ motivation to achieve mastery, create unnecessary test anxiety, and make the scoring and interpreting of results significantly harder for the teacher. Fortunately, there are ways for teachers to eliminate such scenarios.

The key components to constructing good classroom tests are (1) content knowledge, (2) clear learning outcomes, (3) knowledge and awareness of students’ developmental processes and of the cognitive processes invoked by tasks, and (4) an understanding of the properties of different item formats. Constructing classroom tests can be implemented in three major steps: (1) aligning test items to the learning objectives of the unit, (2) following recommended guidelines for test construction, and (3) evaluating the test after test administration. The following are recommended guidelines for general test construction. For specific guidelines regarding specific types of items see sources listed in the References: section at the end of this research-paper.

1. Aligning Test Items to Learning Objectives

Keeping instruction and assessment aligned are important for maximizing student learning. Test blueprints can greatly assist in ensuring that test items assess desired instructional content, include a representative sample of the content, and that the number of items on the test is appropriate given time allocations.

2. Following Recommended Guidelines for Test Construction

Depending on different item formats, recommended guidelines will change (see Kubiszyn & Borich, 2007; Nitko, 2004). There are, however, universal guidelines that can be applied across formats.

1. Provide clear directions.
2. Avoid ambiguous or trick questions.
3. Do not provide unintentional cues in either the item itself, or in other items on the test.
4. Avoid complex or unfamiliar vocabulary or syntax.
5. Use general rules of grammar in constructing items.
6. Check for bias or offensive language.
7. Check for appropriateness of content; do not assess trivial information.
8. Physically format the test appropriately.
9. Arrange items of similar format together to minimize confusion to students and maximize time.
10. Provide proper amount of space for students’ responses.
11. Be consistent when using blanks (FIB), vertically or horizontally displaying alternatives (MC, T/F).
12. Avoid page breaking in the middle of an item.
13. Create the test with enough time to proofread, take the test yourself, and possibly have a colleague review the content.
14. Evaluating the Test After Test Administration

This third step is often omitted from teachers’ routines, primarily due to lack of statistical expertise and lack of time. This step, however, is arguably the most underrated step in test construction for making valid inferences about student learning. If a test is poorly constructed, students will likely perform poorly. Their performance is then interpreted incorrectly, thus affecting instructional and motivational components of learning. Another effect of omitting this step is the future use of unrevised tests. Teachers often recycle tests over multiple years; if there are poor-quality items, they should be revised before readministering. Evaluating tests can also inform the quality of teacher instruction. Sometimes the test is well constructed, but the instruction of the concept may have been inadequate or even absent. Teachers can then make appropriate adjustments to the current test scores, or more optimally, reteach and retest.

Judgmental Review

Popham (2005) discusses two types of item improvement approaches that teachers can take: judgmental and statistical. Judgmental item improvement is more of an informal process that requires teachers to essentially review their tests on their own, with their students, and with colleagues. It is similar to the pretest review, only it takes place after test administration. Asking students what they thought of the test is an excellent method to gauge test quality; however, students are not the experts—teachers are. When using student review, teachers need to use their professional judgment and determine which comments are authentic and which are retaliatory or self-serving.

Statistical Review

Statistical item analysis involves computing the percentage of students who got an item correct (item difficulty); the difference between the percentages of higher scoring and lower scoring students who got the item correct (item discrimination); and with multiple-choice items, an analysis of which scoring students used each alternative. In measurement theory it is assumed that higher scoring students’ scores can be trusted more than lower scoring students scores, therefore it is useful to compare the two groups (item discrimination). More students from the higher scoring group than the lower scoring group should get an item correct because they are said to have more knowledge, relatively speaking. In classroom tests, although it is ideal to have all students do well on a test, examining item discrimination can help find faulty test items. These three procedures can lead to the identification of improperly functioning items, thus leading to more accurate performance results and better future tests. Table 47.3 displays some likely scenarios resulting from an item analysis and how to use the results in conjunction with expert judgment.

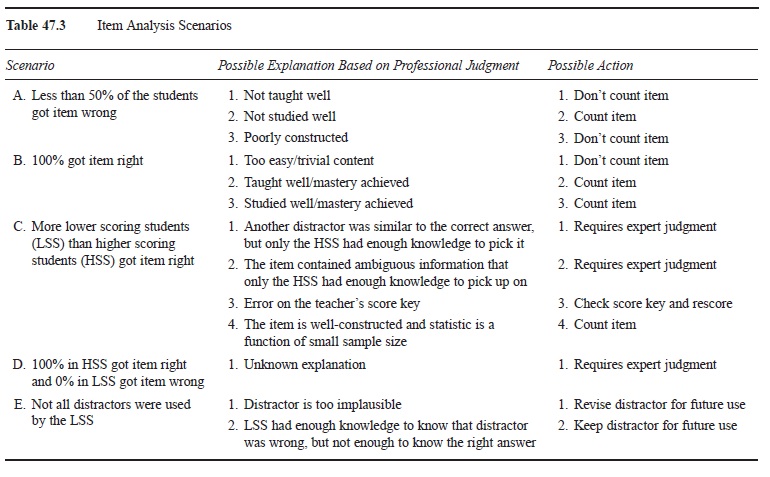Table 47.3       Item Analysis Scenarios

Item analyses are rarely carried out in actual practice, despite their relative benefits. Opponents of classroom level item analyses assert that it assumes too much faith in the isolated results and argue that results are too unstable due to small sample sizes, lack of variation in scores, lack of expertise, and most important, lack of time. Despite these criticisms, when given proper training, teachers ought to statistically evaluate their summative tests and use their expert judgment to draw inferences about test construction. Just because the numerical results signal a potential problem, it does not imply that there actually is a problem. But that judgment should have to be made rather than go completely unnoticed.

Item analyses do take a great deal of time if teachers are to do it by hand rather than through the use of a statistical program. There is, however, a statistical program written by Gordon Brooks available online that will compute an item analysis at http://oak.cats.ohiou.edu/~brooksg/tap .htm (Brooks & Johanson, 2003).

Scoring Tests

Properly prepared tests hold little value if they are not scored adequately. To enhance student learning, the scoring of tests and feedback of test performance should take place in a timely manner. Doing so allows any misconceptions in content to be readily addressed and fixed before moving on to new content.

With objective teacher-made tests, scoring is usually not a problem given their objective nature. Nevertheless, teachers are human and humans make mistakes. Two ways to catch an objective scoring mistake is in an item analysis or through student review of the test items.

Scoring subjective items is of more concern because reliability is at stake. The more subjective an item is, the more unreliable scoring becomes. Ways to increase scoring reliability are to construct clear scoring rubrics before test administration and modify as needed after administration, but before actual scoring, and adhere to the rubric. Often, teachers will spend the time to create a rubric and then not completely follow it, or worse—they won’t create a rubric at all. Although depth of rubrics will vary based on item format, rubrics ought to be created for all constructed response items.

One way to account for scoring reliability is to calculate an interrater agreement coefficient, which involves two or more raters scoring the same items and calculating the proportion of time the raters gave the same score. More details on scoring tests, especially essay tests can be found in the sources listed in the References: section.

Policy Implications

Effects of High-Stakes Testing

The advent of high-stakes testing may have clouded the general advantages of traditional teacher tests. Although standardized tests do not have a direct effect at the classroom level, they do have an indirect effect. Because of the high-stakes nature of many standardized tests, classroom level tests are evolving to mimic their format and content. Also, high-stakes standardized tests have such severe consequences that policy makers and the public have put traditional teacher tests on the back burner. Although there is some evidence that high-stakes tests improve general classroom assessment practices (better and more frequent formative assessment, focus on HOTS), there is also some evidence showing the negative effects (focus on rote learning, increased test preparation) of high-stakes testing (McMillan, 2005). There is, however, little evidence regarding the direct effect of high-stakes testing on the use of teacher-made tests.

One of the more controversial issues is teacher evaluations based on student performance on high-stakes tests. From a more pragmatic perspective it could be argued that if high-stakes tests assess students’ achievement of state standards and teachers teach or assess those standards throughout the year using teacher-made tests, then students should do well on the state tests if they did well on teacher-made tests. Although that is a very tunnel-visioned perspective that creates much debate, the argument suggests that teachers’ use of high-quality, teacher-made tests can have a positive effect on teacher evaluations.

Teacher Assigned Grades

Perhaps traditional teacher tests have received less attention in recent years because of the validity and reliability problems often associated with them. To reiterate, research has shown that teachers lack sufficient knowledge to construct and use test results in valid and reliable ways. Earlier research cited the reasons were due to ineffective training, but recently experts in the field have suggested motivational reasons, suggesting that teachers ignore the recommended measurement guidelines for fear of affecting students’ motivational drive. Teachers have reported that effort and improvement matter, and as teachers it is difficult not to reward students for trying. Although this sounds laudable, it does distort the meaning of grades and teacher-made tests. Good quality tests take a considerable amount of time to construct; to award grades based on nonachievement factors essentially debases all of that time spent.

Teachers frequently report that teacher-made tests account for the majority of assigned grades. If the tests are poorly constructed or inappropriately interpreted, then the grades derived based on those tests are equally poor and inappropriate. The problems of grade inflation, different and unreliable grading scales both within and between schools, can be associated with the need for better accountability measures, thus the standards-based era.

There are reports that high school GPAs have increased, while student performance on standardized tests has not (Reports: Grades improving, 2007). This is not to suggest that teacher-made tests should model standardized tests, but merely to suggest that something is awry in content, instruction, or assessment. If, however, the increase in GPA is due to better instruction, then there is either a possible mismatch between instructional content and standardized test content or the standardized tests are poorly constructed.

Many states offer college financial incentives to students who score high on the state standardized test. Because of low passing rates, however, many states are now devising alternatives for students to qualify for financial scholarships. For example, in some states, a C or better can overrule a passing score on the state test. If this is the case, then teacher-made tests ought to show evidence of both reliability and validity. Some argue that it is detrimental to have such high stakes attached to a single test score, but it is equally detrimental, if not more so, to have such high stakes attached to multiple invalid and unreliable test scores.

Future Directions

The role of teacher-made tests is very different from that of decades ago. Increasingly high-stakes policy implementations and impatient policy makers have shaped the way classroom assessment currently looks. Disconnects between measurement theorists and classroom practitioners has not faded. Teacher preparation programs continue to view classroom assessment as of secondary importance and focus more on alternative methods of assessment, rather than on applying traditional measurement aspects to a realistic classroom environment. While both play vital roles in student learning, both need equal attention in training. Current educators ought to be trained in common measurement techniques so that beginning teachers have a model to follow in their first years of teaching, and measurement theorists need to take into account the role of student-teacher relationships and realistic classroom environments when devising classroom assessment recommendations.

There is no question that teachers want their students to learn in the best ways possible. Various assessment mechanisms provide teachers the tools to help students learn. The difficulty is helping teachers understand how to use each tool efficiently and appropriately. If student learning is to be measured, teachers need to know how and when to use what tools and be able to make useful interpretations within their own context of maximizing time and student learning.

See also:

• How to Write a Research Paper
• Research Paper Topics
• Research Paper Examples

Bibliography:

1. American Federation of Teachers, National Council on Measurement in Education, & National Education Association. (1990). Standards for teacher competence in educational assessment of students. Retrieved July 7, 2007, from http:// www.unl.edu/buros/bimm/html/article3.html
2. Anderson, L. W., & Krathwohl, D. R. (2001). A taxonomy for learning, teaching, and assessing: A revision of Bloom’s original taxonomy of educational objectives. New York: Longman.
3. Black, P., & William, D. (1998a). Assessment and classroom learning. Assessment in Education: Principles, Policy, and
4. Practice, 5(1), 7-77. Black, P., & William, D. (1998b). Inside the black box: Raising standards through classroom assessment. Phi Delta Kappan Online, 80(2), 139-144.
5. Bloom, B. S. (1954). Taxonomy of educational objectives. New York: Longman.
6. Boothroyd, R. A., McMorris, R. F., & Pruzek, R. M. (1992, April). What do teachers know about measurement and how did they find out? Paper presented at the annual meeting of the National Council on Measurement in Education, San Francisco, CA.
7. Brooks, G. P., & Johanson, G. A. (2003). TAP: Test Analysis Program. Journal of Psychological Measurement, 27(4), 303-305.
8. Cizek, G. J., Fitzgerald, S. M., & Rachor, R. E. (1996). Teachers’ assessment practices: Preparation, isolation, and the kitchen sink. Educational Assessment, 3(2), 159-179.
9. Crooks, T. (1988). The impact of classroom evaluation practices on students. Review of Educational Research, 58(4), 438-481.
10. Education Week. (2007). Quality counts 2007: From cradle to career. Bethesda, MD: Author.
11. Frary, R. B., Cross, L. H., & Weber, L. J. (1993). Testing and grading practices and opinions of secondary teachers of academic subjects: Implications for instruction in measurement. Educational Measurement: Issues and Practice, 12(3), 23-30.
12. Kubiszyn, T., & Borich, G. (2007). Educational testing and measurement: Classroom applications and practice (8th ed.). Hoboken, NJ: Wiley.
13. McMillan, J. H. (2001). Secondary teachers’ classroom assessment and grading practices. Educational Measurement: Issues and Practice, 20(1), 20-32.
14. McMillan, J. H. (2005). The impact of high-stakes test results on teachers’ instructional and classroom assessment practices. (ERIC ID: ED490648)
15. McMillan, J. H. (2007). Classroom assessment: Principles and practice for effective standards-based instruction (4th ed.). Boston: Allyn & Bacon.
16. McMillan, J. H., Myran, S., & Workman, D. (2002). Elementary teachers’ classroom assessment and grading practices. The Journal of Educational Research, 95(4), 203-213.
17. McMillan, J. H., & Workman, D. J. (1998). Classroom assessment and grading practices: A review of the literature. (ERIC ID: ED453263)
18. National Council on Measurement in Education. (1995). Code of professional responsibilities in educational measurement. Washington, DC: Author.
19. Nitko, A. J. (2004). Education assessment of students (4th ed.). Upper Saddle River, NJ: Merrill Prentice Hall.
20. Pigge, F. L., & Marso, R. N. (1993, October). A summary of published research: Classroom teachers’ and educators’ attitudes toward and support of teacher-made tests. Paper presented at the annual meeting of the Midwestern Educational Research Association, Chicago, IL.
21. Popham, W. J. (2005). Classroom assessment: What teachers need to know (4th ed.). Boston: Allyn & Bacon.
22. Reports: Grades improving despite weak test scores. (2007, February). CNN.com. Retrieved February 22, 2007, from http://www.cnn.com/2007/EDUCATION/02/22/math in the concept of learning. Education Policy Analysis .reading.scores.ap/index.html?eref=rss_education Archives, 4(17), 345-357.
23. Stiggins, R. J., & Bridgeford, N. J. (1985). The ecology of class room assessment.
24. Tyler, R. W. (1949). Basic principles of curriculum and instruction. Journal of Educational Measurement,. Chicago: University of Chicago. 22(4), 271-286.

Free research papers are not written to satisfy your specific instructions. You can use our professional writing services to order a custom research paper on any topic and get your high quality paper at affordable price.