This sample Connectionism Research Paper is published for educational and informational purposes only. Free research papers are not written by our writers, they are contributed by users, so we are not responsible for the content of this free sample paper. If you want to buy a high quality research paper on any topic at affordable price please use custom research paper writing services.
Abstract
Connectionism is a way of conceptualizing psychological processes that gets its inspiration from the way in which the biological brain processes information. In this approach, psychological phenomena are explained in terms of activations of interconnected neuron-like units whose operations are governed by simple rules.
Outline
- Introduction
- General Features of the Connectionist Cognitive Architecture
- Localist and Distributed Representational Systems and Their Properties
- Dynamics of an Information Processing Unit
- Dynamics of Interunit Connections
- Examples of Connectionist Architectures
- Applications of Connectionism
1. Introduction
Although ideas akin to connectionism may be attributed to past thinkers such as Aristotle and William James, modern connectionism began its tenure during the mid-20th century. Alongside the theoretical and actuarial development of digital computing based on von Neumann’s concept of serial computing (most current computers are of this type), there emerged a research tradition that took seriously the biological brain as a metaphor for information processing. In this view, just as the brain does its work through neurons and synaptic links, the mind too may be conceptualized as functioning through neuron-like simple units and connections among them. Connectionism, also known as neural networks, is so called due to the network of connections among the neuron-like units that are postulated to explain psychological phenomena.
McCulloch and Pitts, Hebb, and Rosenblatt conducted their pioneering work during the 1940s and 1950s. Nevertheless, Minsky and Papert pointed out in 1969 that some of the simple logical operations such as ‘‘exclusive or’’ cannot be performed by the then available mechanisms. These limitations, together with the development of serial computers as a main technological tool of computation, resulted in a decline in the research on brain-inspired information processing mechanisms. While Anderson, Fukushima, Grossberg, Kohonen, and others continued to work during the 1960s and 1970s, it was the 1980s that witnessed the renaissance of connectionism. A mechanism called the generalized delta rule, which rectified connectionism’s problem identified by Minsky and Papert, was developed. A network of simple neuron-like units was shown to be able to model psychological processes such as perception, memory, and learning. Rumelhart and colleagues’ Parallel Distributed Processing, published in 1986, popularized the connectionist approach.
By this time, however, the approach that used the von Neumann serial computer as a metaphor of mind (a psychological process is considered to be a series of discrete steps of mental operations on some mental representations) had established itself as the dominant research program in psychology and cognitive science. Controversies ensued as to how connectionism differs from the serial processing approach, which approach explains psychological processes better, and whether connectionism provides a realistic model of brain processes.
2. General Features Of The Connectionist Cognitive Architecture
Although connectionist architectures vary considerably, they can be characterized in general terms. First, a connectionist network typically consists of a large number of units (sometimes called nodes) that are connected to each other with varying strengths (Fig. 1). The operation of each unit is governed by a simple rule (discussed later) that determines its activation state (‘‘firing’’ or ‘‘resting’’) as a function of the inputs it receives from the connected units. The connection strength (often called weight) of a given unit to another unit indicates the amount of influence the first unit has over the second unit. Second, the pattern of activation of the units changes over time. The rules used in connectionist networks specify how the activation of a unit at one point in time (t) affects other units at a later time (t + Dt). Interunit effects occur in parallel, so that during a given time interval (Dt), the effects of all units on other units (a unit may have an effect on itself) take place. As a result, the state of a connectionist network can continue to change, potentially forever. However, under some circumstances, the state of a connectionist network shows a discernible temporal pattern. For instance, it may come to a stable pattern, oscillate between two or more patterns, or exhibit a chaotic pattern. Third, a connectionist network performs its function collectively. If one unit is activated, its activation spreads via its connections to other units in accordance with a rule. As these activations reverberate through the network, the network as a whole may then perform various functions such as the encoding and retrieval of information.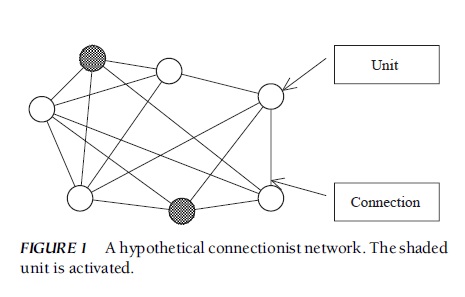
FIGURE 1 A hypothetical connectionist network. The shaded unit is activated.
Connectionism differs from models of cognition based on the serial computer metaphor in several respects. A serial computer typically has a central processing unit (CPU), data, and procedures (i.e., software) that operate on the data, and the CPU executes the procedures to handle the data. One fundamental assumption of the serial computer metaphor of cognitive processes is that both data and procedures are written in terms of physical symbols. Physical symbols (e.g., the word ‘‘cat’’) refer to or stand for some objects and events in the world (e.g., the cat on the mat) and are themselves physically coded on a physical medium such as an ink mark on paper, an electronic circuit, or a synaptic circuit in the brain. In contrast, connectionism does not assume the existence of a single CPU; rather, it assumes the existence of a multitude of simple processing units. What the CPU does in a serial computer is governed by a simple or complex set of procedures that can be programmed (e.g., a simple calculator, complex word processing software), but processing units in connectionist networks have a simple and fixed rule. In other words, connectionist networks are not programmable in the same way in which a serial computer can be programmed—although they can be trained or taught (discussed later). Finally, connectionism does not assume the explicit coding of information in physical symbols. Despite these differences, both metaphors have been fruitfully used to advance psychological science. One metaphor appears to be more suited to model some psychological processes than to model others, but both metaphors often do a similarly good job of explaining a set of phenomena. At this point in history, they may be best considered to be different research programs with different theoretical assumptions and conventions rather than two competing paradigms.
Although neurally inspired, connectionist networks are not models of brain functions. Put differently, the relationship between the connectionist network and the brain is metaphorical rather than literal. To be sure, connectionist modelers often make use of design principles that are observable in the brain. For instance, just as the firing of a neuron is not a simple linear function of the excitation it receives, the activation of a unit in a neural network is often governed by a nonlinear function of the inputs it receives. Just as synaptic connections may be excitatory or inhibitory, connections among connectionist units may be excitatory or inhibitory. However, a learning rule such as the generalized delta rule, which plays an important role in neural network research, has no known corresponding mechanism in the brain. More generally, the brain anatomy is highly structured, but most neural networks do not have differentiated architectures that resemble the brain structure. In the long run, neural network research may become more informed by neuroscience (and, in fact, there is research that tries to model brain functions). Currently, however, connectionist networks are at best highly abstracted and stylized models of how the brain works. For this reason, connectionist networks are often called artificial neural networks.
3. Localist And Distributed Representational Systems And Their Properties
How do we understand objects and events in the world, and how do we experience our world as meaningful? Meaning is one of the most important questions for models of cognition. In cognitive models based on the serial computer metaphor, symbols gain their referential meanings by designation; a symbol is designated to refer to a certain object or event in the world. In this sense, meaning is built into the system of cognition. In neural networks, meaning is handled in two different ways. The localist approach is akin to the serial models of cognition. Here, a unit in a connectionist network is designated to have its referent. When this unit is activated, the person is considered to be in some sense ‘‘thinking about’’ the referent that the unit represents. In contrast, in the distributed approach, any given unit might not have a clear referent, and its activation cannot be interpreted as corresponding to any meaningful thought in and of itself. Rather, it is a pattern of activations of many units that imply a meaning. In other words, meaning is not localized to a unit but rather distributed across units. A unit in a distributed system then represents some microfeature of a meaningful concept that may or may not be interpretable using symbols such as words and phrases. In this sense, a distributed approach models subsymbolic processes.
An advantage of the localist approach is its ease of interpretation. The activation of a unit means that the concept represented by the unit is being thought about; changes in activation of a network can be easily interpreted as changes in the content of thought. Although the localist approach may be sufficient to model many psychological processes, the distributed approach might be necessary when some of the following features are important. First, the distributed representational system has a built-in capacity to model similarity. Because a concept is represented by a pattern of unit activation in the distributed system, the similarity between one pattern and another pattern of activation can be naturally interpretable as a similarity in meaning. Second, the capacity to represent similarity enables the distributed system to have the capacity for psychological generalization as an inherent aspect of the system. If a system responds to a pattern in a certain way, it responds to a similar pattern in a similar way; that is, the system generalizes as a natural consequence of its distributed format. Third, these capacities often result in a graceful degradation if the system is damaged. For instance, if one unit in a localist network is damaged or removed, it loses the capacity to represent the corresponding concept. However, even if one unit in a distributed network is lost, it still retains most of the capacity to represent concepts even though the clarity of representation might be compromised to some extent.
4. Dynamics Of An Information Processing Unit
In a time interval (Dt), an information processing unit in a neural network receives inputs from other units, computes its net inputs, gets activated according to an activation function, and sends out its output to other units according to an output function. Figure 2 shows a schematic picture in which Unit i receives inputs from its neighbors, Unit j and other connected units, and sends out its output. When a neighboring Unit j sends out its output, oj, it spreads via the connection with its connection strength or weight, wij, to Unit i. The input from j to i then is the product of the output and weight, that is, wijoj. The inputs from other units are also computed in a similar fashion. The Unit i then sums all inputs to compute its net input, that is, neti = Ewijoj, where the summation is over j, which indexes units that send out their outputs to Unit I.
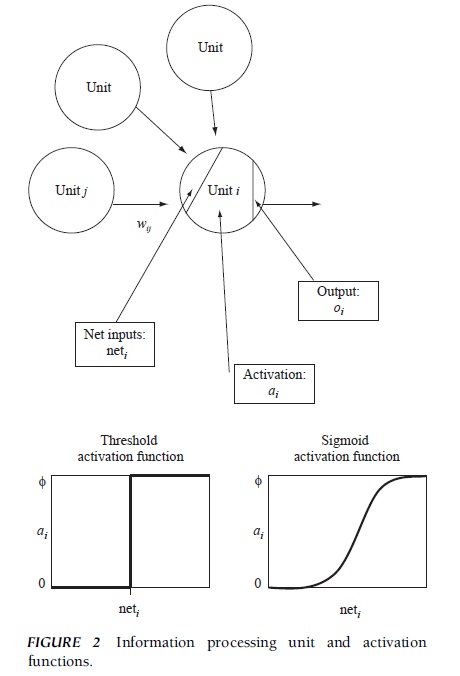FIGURE 2 Information processing unit and activation functions.
Whether, or how much, Unit i is activated depends on the net input and the activation function of the unit. Typically, the resting state of a unit is indicated by the activation level of zero and the firing state is 1; however, depending on the architecture, a unit may take a value between –1 and +1 or between negative and positive infinity. The activation function determines activation level of the unit as a function of net inputs. Although activation function may be a simple linear function, it often takes a nonlinear form. One example is a threshold function (lower left panel of Fig. 2), where the activation level remains zero if the net inputs remain lower than a threshold value but its level becomes 1 when the net inputs exceeds the threshold.
Another example is a sigmoid function, where activation changes smoothly as a function of net inputs in the shape depicted (lower right panel of Fig. 2). These nonlinear activation functions are critical in some applications. The output of Unit i is determined by the activation level of the unit and its output function. Although output is often identical to activation (i.e., oi = ai), it may vary for some applications.
When activation spreads in only one direction (i.e., from Unit j to Unit i), activation feeds forward from one set of units to another set in one time interval, whose activation then spreads to a third set in the next interval, and so on. This type of network, called a feedforward network, basically transforms one set of activations in the first set of units into another set of activations in the last set of units. Its main function is to convert one set of signals to another set of signals. In psychological terms, it may be useful, for instance, for modeling how a given situation or stimulus may induce a set of responses. However, activation may spread bidirectionally (from Unit j to Unit i as well as from Unit i to Unit j), and the connection strength in one direction may or may not be the same as that in the opposite direction. In these cases, more complex dynamics emerge where activation may spread back and forth and reverberate through the network. This type of network, sometimes called a recurrent network, may tend toward a stable pattern of activation in which activation levels of the units change little or oscillate among several stable patterns. These networks may be used to model memory retrieval processes. Recurrent networks may sometimes exhibit an even more complex pattern known as chaos.
5. Dynamics Of Interunit Connections
Interunit connections in a connectionist network may be fixed or modifiable. In the latter case, connections are modified in accordance with a learning rule, so that the network may learn contingencies among events in its environment. For illustrative purposes, let us consider a simple example of a distributed feedforward network with two layers. In this network, each layer has three units and there is no connection among the units within each layer, but all of the units in one layer are fully connected to the units in the other layer (Fig. 3). Let us suppose that the network is to learn that when Event A happens, Event B follows. Further assume that Event A is encoded by the units in the first layer; when the first unit is activated (+1) but the other units are not activated (0), this means that Event A is represented in the network. Event B is encoded by the units in the second layer; when the first unit in this layer is not activated (0) but the second and third units are activated (+1), this means that Event B is represented in the network.
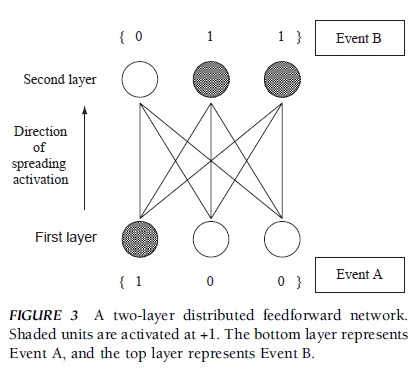FIGURE 3 A two-layer distributed feedforward network. Shaded units are activated at +1. The bottom layer represents Event A, and the top layer represents Event B.
For the network to learn the association between Event A and Event B, the network needs to modify its connections so that when Event A is represented in the first layer, its activation would spread to the second layer and Event B should then be represented in the second layer. There are two basic types of learning rules that can accomplish this. One is called unsupervised learning, and the typical learning rule is called the Hebbian learning rule, named after the psychologist Donald Hebb. The rule is to strengthen the connection between the units that are activated at the same time. In this example, the connections between the first unit in the first layer and the second and third units in the second layer should be strengthened (e.g., from 0 to 1), whereas the other connections should remain unchanged (e.g., 0). In this case, assuming that input, activation, and output all are the same for a given unit, it is easy to see that the pattern of activation {1 0 0} in the first layer would spread to the second layer and activate the second and third units but would not activate the first unit in the second layer. More formally, this rule is more generally expressed by the following equation: Dwij = eaioj, where Dwij is the amount of change in connection strength from Unit j to Unit i, ai is the activation level of Unit j, oj is the output of Unit j, and e specifies a learning rate, that is, the parameter that governs the speed of learning.
The other type of learning is called supervised learning, for which the typical rule is the delta (or back propagation) rule. Here, the connections are changed so that if Event A is represented in the first layer, it predicts Event B in the second layer. Event B acts as a ‘‘teacher’’ that is to be emulated by the network. Here is how the rule works. Assuming that all of the connection strengths are initially zero, all of the inputs to the units in the second layer would be zero. For the first unit in the second layer, then, the teacher is zero and the activation is also zero, that is, no error. When there is no error, the connection strengths remain the same. So, the connections coming into the first unit in the second layer remain zero. However, the teacher for the second and third units says that they should be activated (i.e., +1) even though they are not activated (i.e., 0). The difference between the teacher and the predicted activation is an error, which is then used to modify the connection strength. The rule is to change the connection strength to reduce the error so that the connection with the activated unit gets stronger but that with the resting unit remains the same. Therefore, the connection from the first unit in the first layer to the second and third units in the second layer is strengthened (e.g., from 0 to +1), but the other connections remain unchanged (e.g., 0). Again, this rule can modify the connection strengths appropriately so that the network predicts Event B when Event A is encoded. More generally, this rule is expressed by the following equation: Dwij = e(ti–ai)oj, where Dwij is the amount of change in connection strength from Unit j to Unit i, ti is the teacher’s activation level, ai is the predicted activation level of Unit j, oj is the output of Unit j, and e is the learning rate. At one level, supervised learning differs from unsupervised learning in the presence of a teacher or supervisor in the learning process. Supervised learning is sometimes said to be less realistic because people learn without being told what they have expected is wrong by how much. However, even with supervised learning rules, there is no need to postulate the explicit presence of a human teacher. The only necessary assumption is that one of the events to be associated is regarded as a teacher. In other words, the ‘‘teacher’’ may be a human, a machine, or nature. More significantly, supervised and unsupervised learning rules differ in terms of their conceptualization of learning. On the one hand, unsupervised learning conceptualizes learning as the observation and learning of the co-occurrence of events in the world.
On the other hand, supervised learning presupposes a learning agent that implicitly predicts what follows what (e.g., Event B follows Event A) and learns from mistakes. In this sense, supervised learning may be able to model adaptation. However, networks with supervised learning may actually be too adaptive in that they might forget previously learned associations—sometimes even catastrophically—when new associations are learned. Unsupervised learning does not have this problem most of the time. Both the Hebbian and delta rules can be generalized to more complex forms.
6. Examples Of Connectionist Architectures
A tensor network is an example of the connectionist architecture that embodies a generalized form of the Hebbian learning rule (Fig. 4). In the example in the previous section, the network learned the association between two events, but a tensor network is designed to learn to associate three or more events (Fig. 4 depicts a network that associates three events). One cluster of units represents one type of event, the units in one cluster are connected to the units in other clusters, and the connection among units (the connection among three units in Fig. 4) changes as a function of the activation levels of those units. This type of network is called a tensor network because the learning rule can be mathematically described by a mathematical representation called tensor. When one of the clusters of units is activated, its activation spreads to other units, which are then activated to retrieve stored information. A tensor network is suitable for integrating multiple pieces of information into a structured representation. It can bind together different types of information such as color, time of blooming, and habitat; for instance, it can represent the name of a red flower that blooms during the early spring in wetlands. More generally, a tensor network can approximate the intersection of different sets.
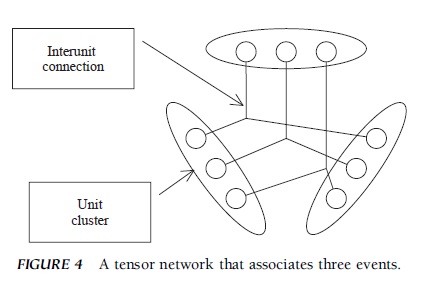FIGURE 4 A tensor network that associates three events.
A multilayer feedforward network is an example of the architecture that uses a generalized form of the delta rule (Fig. 5). In the previous example, there were two layers of units, but a multilayer network has three or more layers of units. The first and last layers are called input and output layers because they interface with the environment, encoding the incoming information (input layer) and decoding the outgoing response (output layer). The middle layers are called hidden layers because they are hidden from the environment. When the input layer units are activated, their activation spreads to the hidden layer units, which are then activated. The activation feeds forward so that the output layer units are activated. The output layer activation is compared to the relevant teacher, and the discrepancy (error) is then used to modify the connection strengths among the units. First, the connections between the output layer units and the units in the next last layer are modified, then the connections between the next last layer and the units before this layer (input layer in Fig. 5) are modified, and so on. Thus, the error information propagates backward, so to speak, to modify the connections. This is why the generalized delta rule is also called the a hidden layer is useful for transforming an input representation to re-represent it.
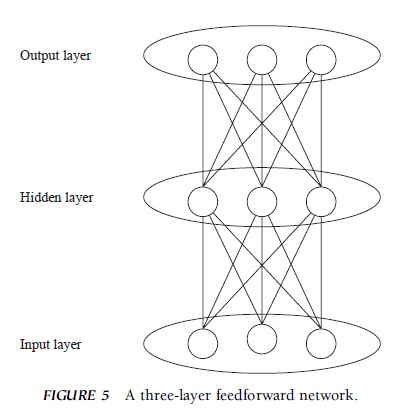FIGURE 5 A three-layer feedforward network.
Some architectures use the Hebbian or delta rule with further modifications to the basic network structure. In recurrent networks (sometimes called autoassociative networks), units may have connections that spread activation not only in one direction but also in the opposite direction. This type of architecture tends to amplify strong activation and dampen weak activation, sharpening the pattern of activation. It can be used for pattern completion; that is, when only a part of the original information is presented, this network can often fill in the missing part to complete the original pattern. Its practical uses include noise reduction and error correction.
Although these types of connectionist networks are based on somewhat different conceptions of learning and have different advantages and disadvantages, they may be combined to model more complex processes. A complex network that combines different types of network architectures is sometimes called a modular architecture. Each module is designed to perform a specified function, whose output is then used by another module for further processing. For example, a recurrent network may be used to clean noisy inputs so as to provide a clearer input to a tensor network, whose output may then be transferred to a multilayer feedforward network for modeling adaptive learning. Several modules may then function in tandem to provide a more complete model of human and animal psychological processes.
7. Applications Of Connectionism
Connectionist networks provide versatile research tools for developing a model of human psychological processes. For example, they have been used to model some basic perceptual and cognitive processes such as pattern recognition, learning, memory, categorization, judgment and decision making, and natural language processing as well as more social psychological processes such as person impression formation, stereotyping, causal attribution, and stereotype formation and change. Some models have been used to discuss issues pertaining to developmental psychology. Some networks have been used to model neuropsychological issues; when parts of the interunit connections of a network are removed, the network exhibits behaviors that are similar to those of people with brain lesions. Other variants can model animal behaviors as well. Although more applied areas of psychological research have been relatively slow to embrace connectionism, there are some signs of its use. Finally, the technology used in connectionist networks has been adopted not only to model psychological processes but also for engineering or other purposes. For instance, optic pattern recognition is useful for machine pattern recognition, and feedforward networks may be used for forecasting.
References:
- Anderson, J. A., & Rosenfeld, E. (1988). Neurocomputing. Cambridge, MA: MIT Press.
- Elman, J. L., Bates, E. A., Johnson, M. H., Karmiloff-Smith, A., Parisi, D., & Plunkett, K. (1998). Rethinking innateness: A connectionist perspective on development. Cambridge, MA: MIT Press.
- Minsky, M., & Papert, S. (1969). Perceptrons. Cambridge, MA: MIT Press.
- Read, S. J., & Miller, L. C. (1998). Connectionist models of social reasoning and social behavior. Mahwah, NJ: Lawrence Erlbaum.
- Rumelhart, D. E., & McClelland, J. L., & the PDP Research Group. (1986). Parallel distributed processing. Cambridge, MA: MIT Press.
See also:
Free research papers are not written to satisfy your specific instructions. You can use our professional writing services to order a custom research paper on any topic and get your high quality paper at affordable price.
ORDER HIGH QUALITY CUSTOM PAPER
Always on-time
Plagiarism-Free
100% Confidentiality
